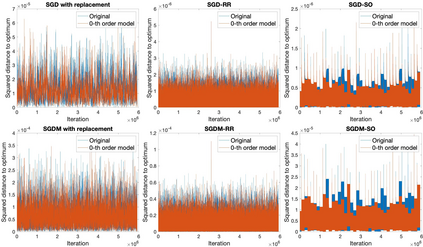
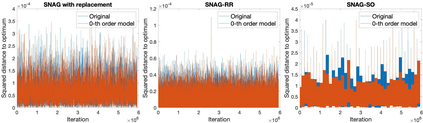
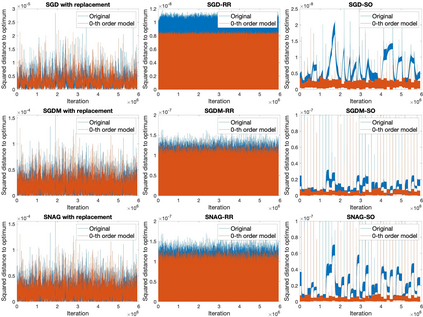
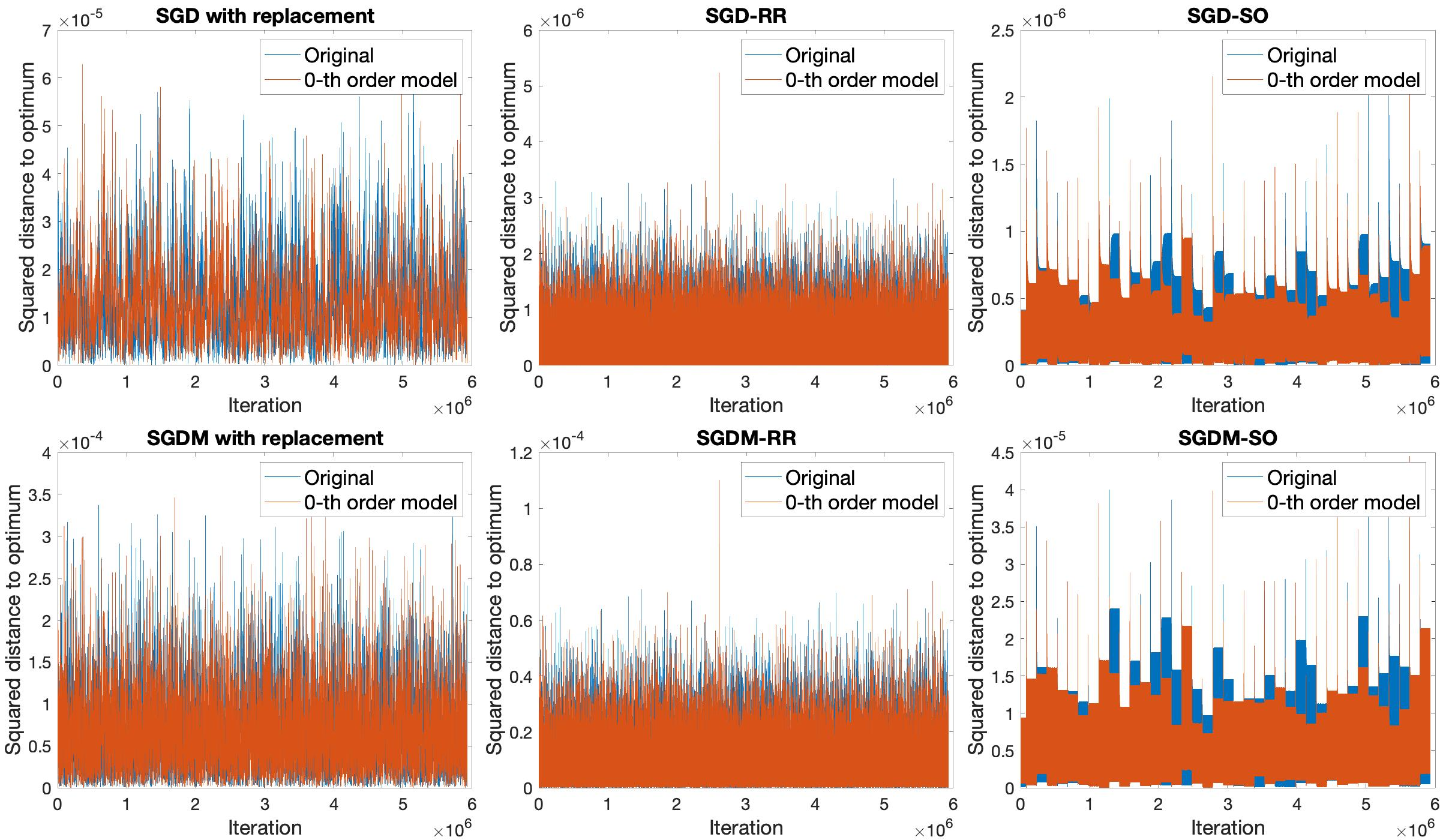
When solving finite-sum minimization problems, two common alternatives to stochastic gradient descent (SGD) with theoretical benefits are random reshuffling (SGD-RR) and shuffle-once (SGD-SO), in which functions are sampled in cycles without replacement. Under a convenient stochastic noise approximation which holds experimentally, we study the stationary variances of the iterates of SGD, SGD-RR and SGD-SO, whose leading terms decrease in this order, and obtain simple approximations. To obtain our results, we study the power spectral density of the stochastic gradient noise sequences. Our analysis extends beyond SGD to SGD with momentum and to the stochastic Nesterov's accelerated gradient method. We perform experiments on quadratic objective functions to test the validity of our approximation and the correctness of our findings.
翻译:在解决有限和最小化问题时,两种具有理论效益的随机重整(SGD-RR)和冲洗(SGD-SO)是具有理论效益的随机重整(SGD-RR)和冲洗(SGD-SO)的常见替代物,其功能在循环中取样,而没有替换。在一种方便的随机噪声近似条件下,我们实验SGD、SGD-RR和SGD-SO的迭代物的固定差异,其主要条件在此顺序下下降,并获得简单的近似值。为了获得结果,我们研究了随机梯度噪声序列的能量光谱密度。我们的分析从SGD到SGD,以动力延伸至SGD,再延伸至SGD,以及Schachatic Nesterov的加速梯度方法。我们在四边目标功能上进行实验,以检验我们近似值的有效性和我们发现结果的正确性。