Bayesian high-dimensional covariate selection in non-linear mixed-effects models using the SAEM algorithm

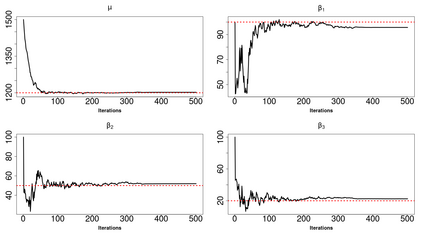
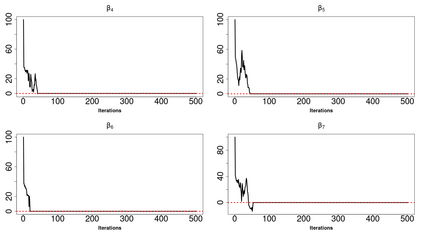
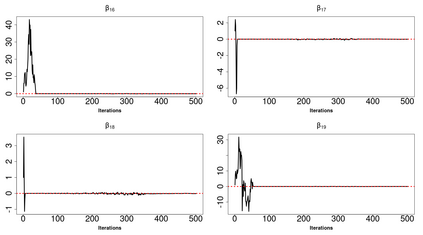
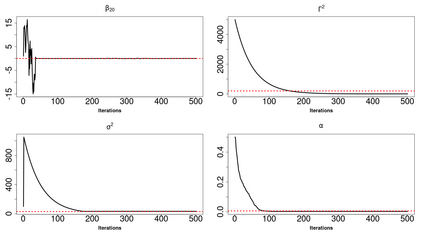
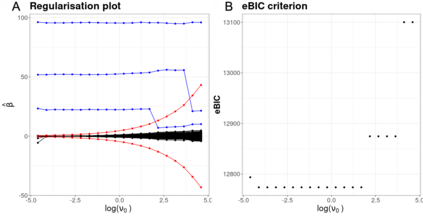
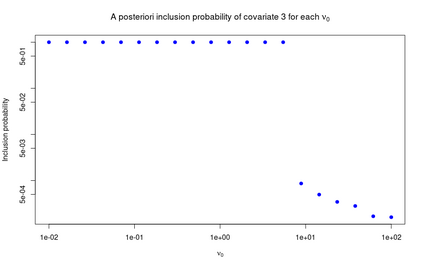
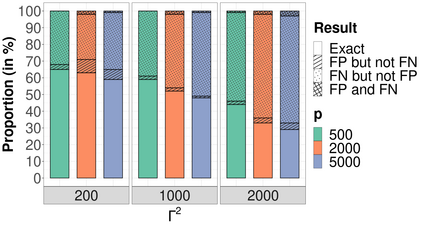
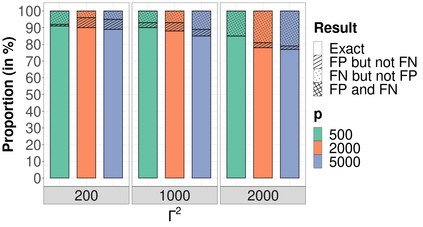
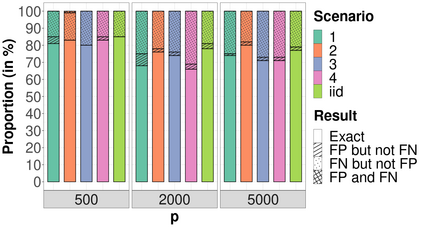
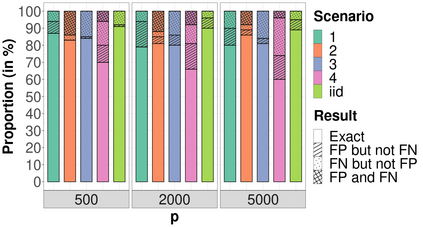
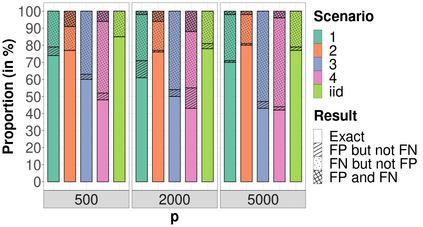
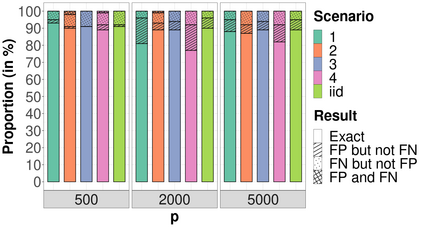
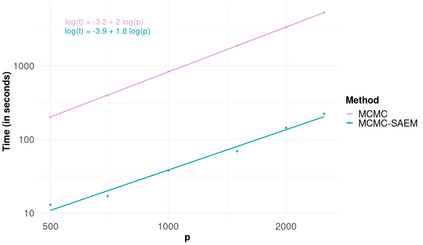
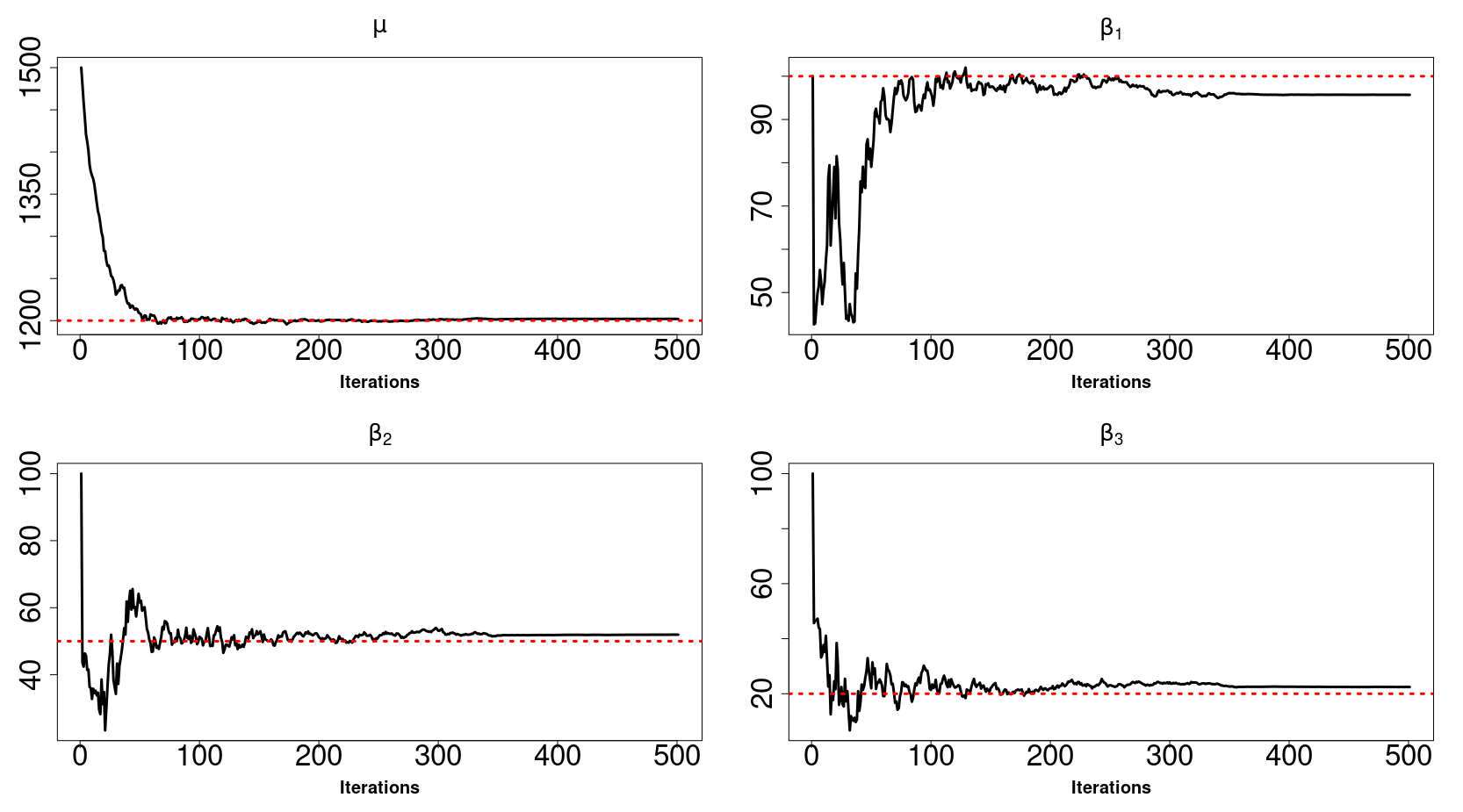
High-dimensional data, with many more covariates than observations, such as genomic data for example, are now commonly analysed. In this context, it is often desirable to be able to focus on the few most relevant covariates through a variable selection procedure. High-dimensional variable selection is widely documented in standard regression models, but there are still few tools to address it in the context of non-linear mixed-effects models. In this work, variable selection is approached from a Bayesian perspective and a selection procedure is proposed, combining the use of spike-and-slab priors and the SAEM algorithm. Similarly to LASSO regression, the set of relevant covariates is selected by exploring a grid of values for the penalisation parameter. The proposed approach is much faster than a classical MCMC algorithm and shows very good selection performances on simulated data.