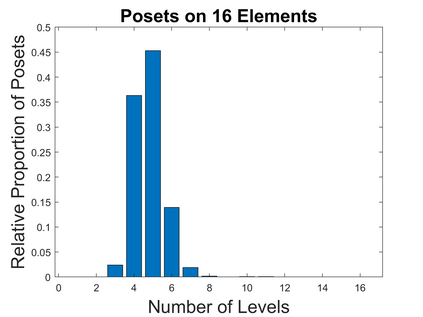
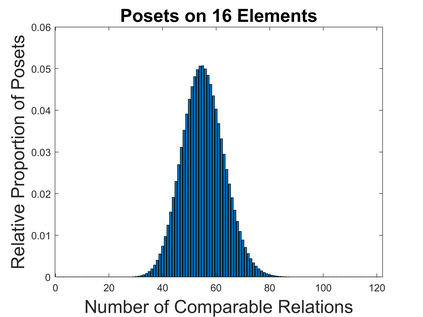
We investigate causal inference in the asymptotic regime as the number of variables approaches infinity using an information-theoretic framework. We define structural entropy of a causal model in terms of its description complexity measured by the logarithmic growth rate, measured in bits, of all directed acyclic graphs (DAGs), parameterized by the edge density d. Structural entropy yields non-intuitive predictions. If we randomly sample a DAG from the space of all models, in the range d = (0, 1/8), almost surely the model is a two-layer DAG! Semantic entropy quantifies the reduction in entropy where edges are removed by causal intervention. Semantic causal entropy is defined as the f-divergence between the observational distribution and the interventional distribution P', where a subset S of edges are intervened on to determine their causal influence. We compare the decomposability properties of semantic entropy for different choices of f-divergences, including KL-divergence, squared Hellinger distance, and total variation distance. We apply our framework to generalize a recently popular bipartite experimental design for studying causal inference on large datasets, where interventions are carried out on one set of variables (e.g., power plants, items in an online store), but outcomes are measured on a disjoint set of variables (residents near power plants, or shoppers). We generalize bipartite designs to k-partite designs, and describe an optimization framework for finding the optimal k-level DAG architecture for any value of d \in (0, 1/2). As edge density increases, a sequence of phase transitions occur over disjoint intervals of d, with deeper DAG architectures emerging for larger values of d. We also give a quantitative bound on the number of samples needed to reliably test for average causal influence for a k-partite design.
翻译:我们用一个信息理论框架来调查无线系统中的因果推断,因为变量的数量会随着信息-理论框架的无限化而变化。我们定义了因果模型的结构变异性,其描述复杂性是以所有定向环状图(DAGs)的对数增长率(以位计)测量的,其参数是边缘密度 d. 结构变异产生非直观的预测。如果我们随机地从所有模型的空间,在范围 d = (0, 1/8) 中抽取一个DAG,该模型几乎肯定是一个双层DAG! 语义变异性变异性使因果模型的变异性变异性(包括KL-Rationrence), 数值变异性变异性变异性变异性变异性变异性变异性变异性变异性变异性变性变异性变异性(在常规变异性变异性变异性变异性变异性变异性变异性变异性变异性变性变异性变变变变性变异性变变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变性变变性变性变变变变变变变变变变变性变性变性变性变性变性变变变变变