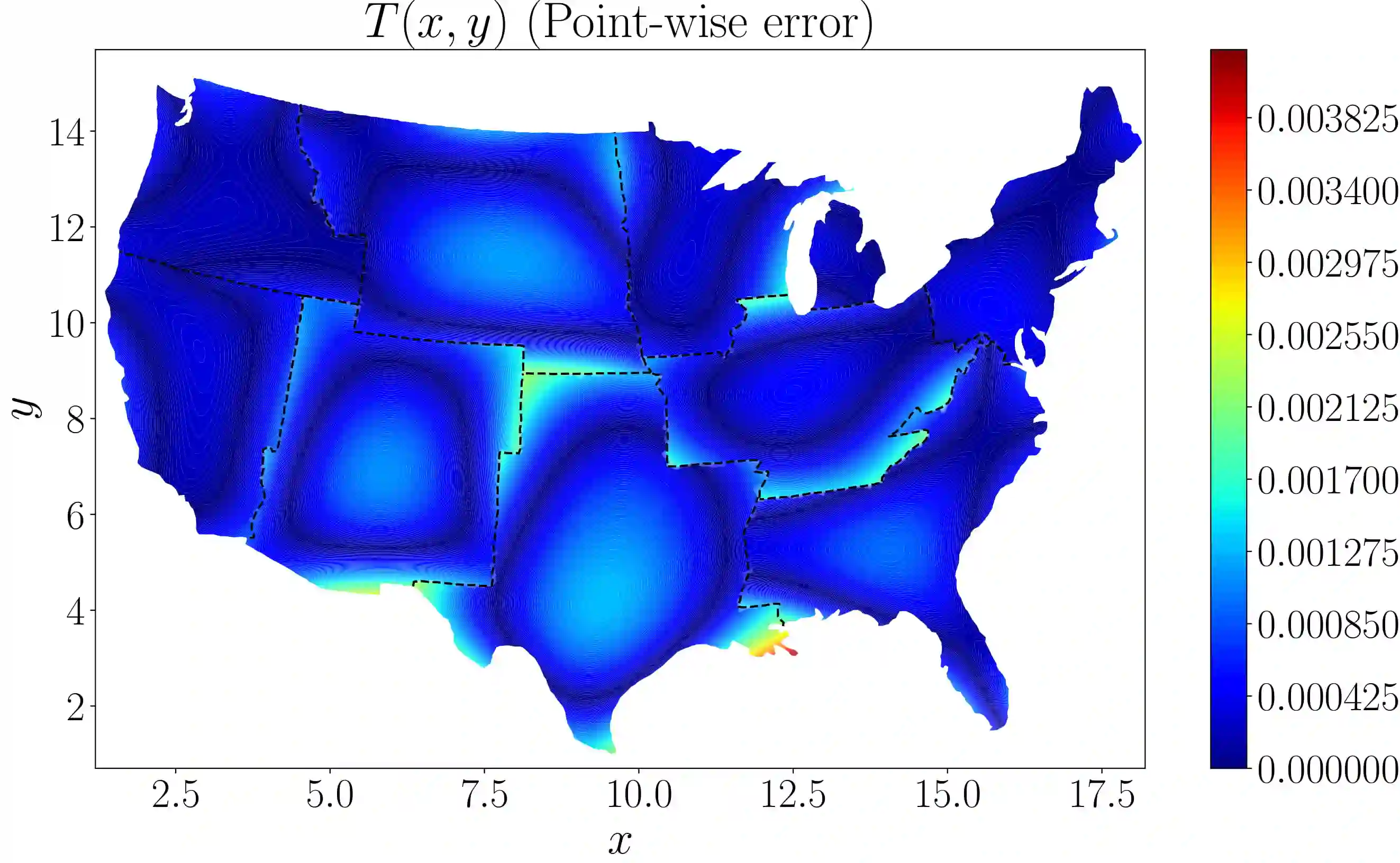
We develop a distributed framework for the physics-informed neural networks (PINNs) based on two recent extensions, namely conservative PINNs (cPINNs) and extended PINNs (XPINNs), which employ domain decomposition in space and in time-space, respectively. This domain decomposition endows cPINNs and XPINNs with several advantages over the vanilla PINNs, such as parallelization capacity, large representation capacity, efficient hyperparameter tuning, and is particularly effective for multi-scale and multi-physics problems. Here, we present a parallel algorithm for cPINNs and XPINNs constructed with a hybrid programming model described by MPI $+$ X, where X $\in \{\text{CPUs},~\text{GPUs}\}$. The main advantage of cPINN and XPINN over the more classical data and model parallel approaches is the flexibility of optimizing all hyperparameters of each neural network separately in each subdomain. We compare the performance of distributed cPINNs and XPINNs for various forward problems, using both weak and strong scalings. Our results indicate that for space domain decomposition, cPINNs are more efficient in terms of communication cost but XPINNs provide greater flexibility as they can also handle time-domain decomposition for any differential equations, and can deal with any arbitrarily shaped complex subdomains. To this end, we also present an application of the parallel XPINN method for solving an inverse diffusion problem with variable conductivity on the United States map, using ten regions as subdomains.
翻译:我们根据两个最近的扩展,即保守的PINNs(cPINNs)和扩展的PINNs(XPINNs),为物理知情神经网络(PINNs)开发一个分布框架,分别使用空间和时空的域分解。这个域分解内含 CPINs 和 XPINNs,比香草 PINNs具有若干优势,例如平行能力、大型代表能力、高效超参数调,对于多尺度和多物理问题特别有效。在这里,我们为 CPINs和扩展的PINNs(XPNNNN) 提供了一种平行的算法,用混合的编程模型X$+$+$X, X$$@text{CPUs},{gtext{GPUs ⁇ $$。clations 和XPINNN(XPNN)相对于较经典的数据和模型平行方法的主要优势是,在每一个子领域分别优化每个复杂的神经网络的超参数。我们比较了已分发的CPN和XPNNNNNS应用的运行的功能, 和XPNPNNNNNNNNNNPs在各种前方平面的进度中也显示一种较强的动作的灵活性。