CAN-PINN: A Fast Physics-Informed Neural Network Based on Coupled-Automatic-Numerical Differentiation Method

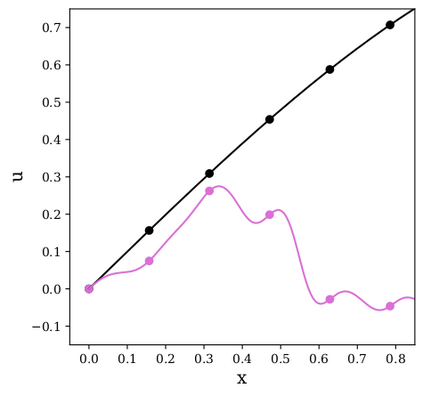
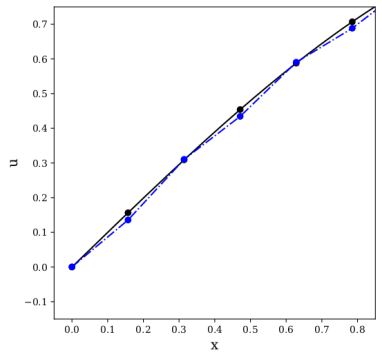
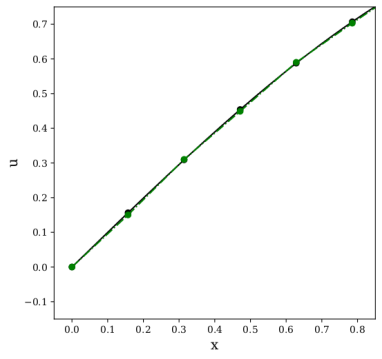
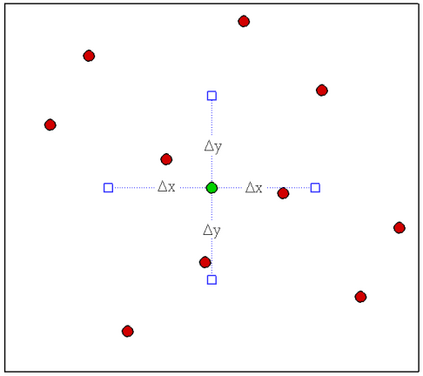
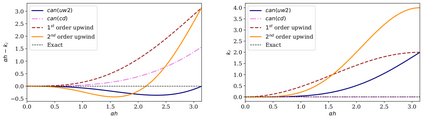
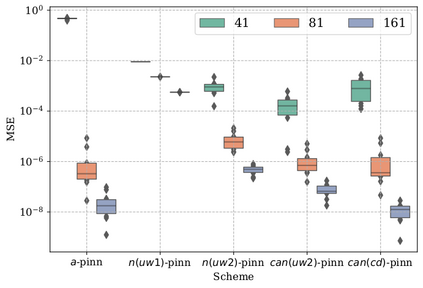
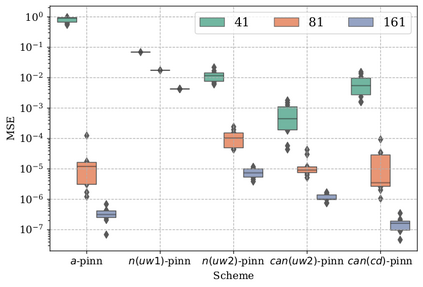
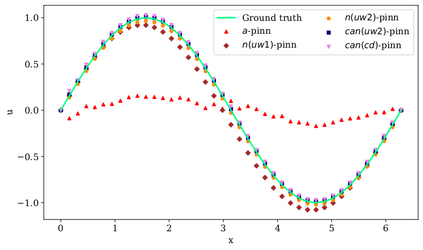
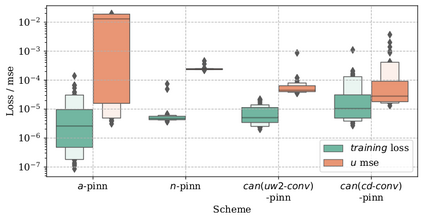
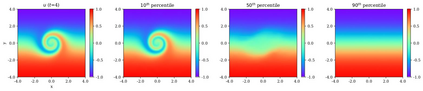
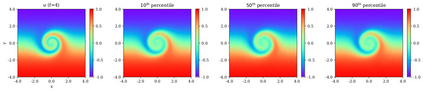
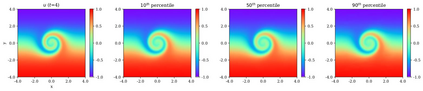
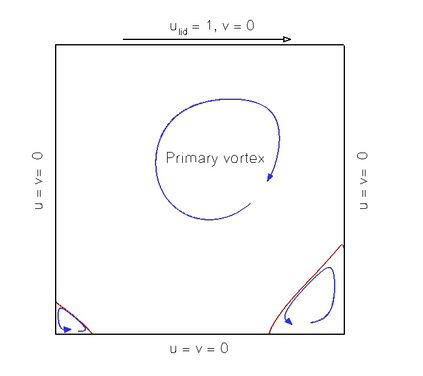
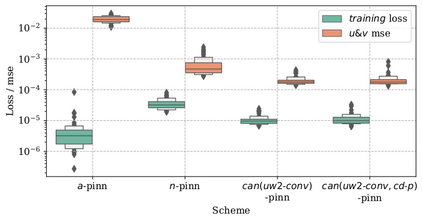
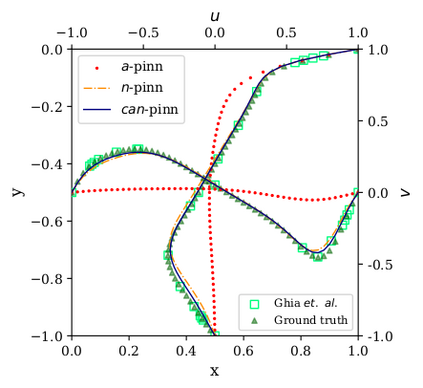
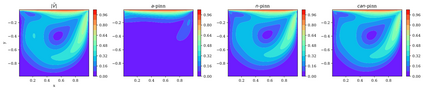
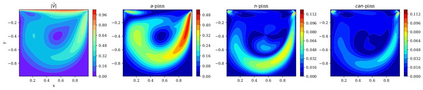
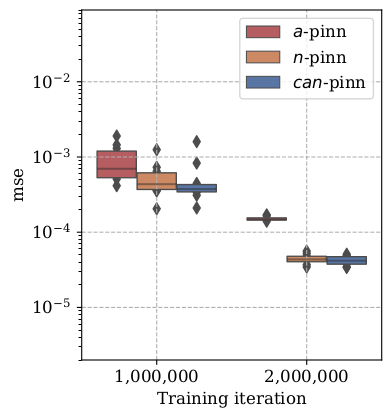
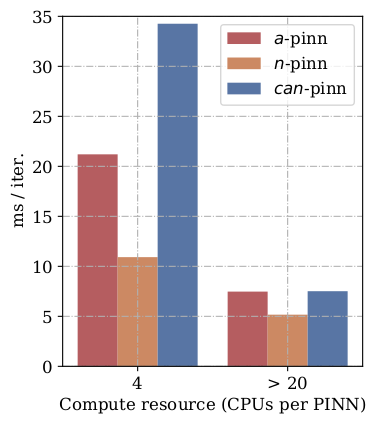
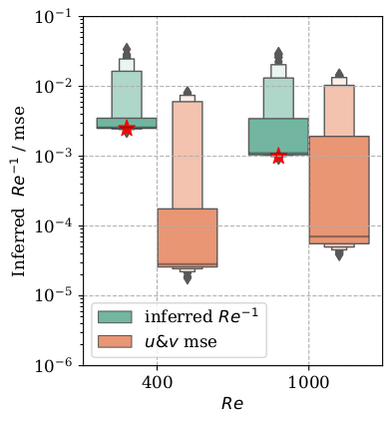
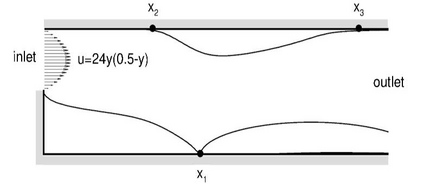
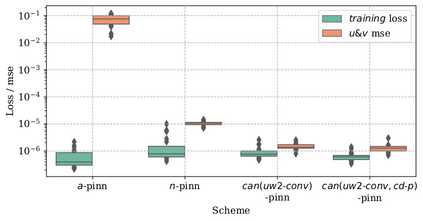
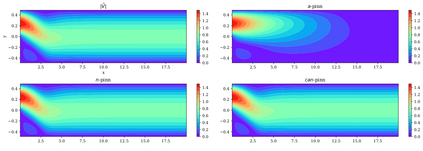
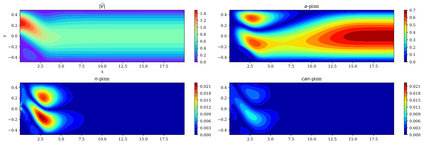
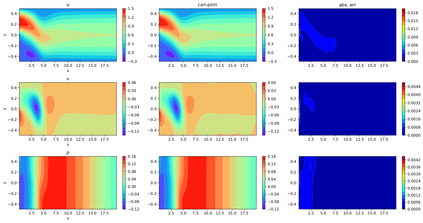
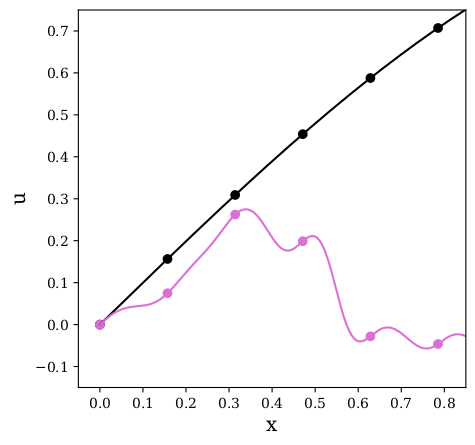
In this study, novel physics-informed neural network (PINN) methods for coupling neighboring support points and automatic differentiation (AD) through Taylor series expansion are proposed to allow efficient training with improved accuracy. The computation of differential operators required for PINNs loss evaluation at collocation points are conventionally obtained via AD. Although AD has the advantage of being able to compute the exact gradients at any point, such PINNs can only achieve high accuracies with large numbers of collocation points, otherwise they are prone to optimizing towards unphysical solution. To make PINN training fast, the dual ideas of using numerical differentiation (ND)-inspired method and coupling it with AD are employed to define the loss function. The ND-based formulation for training loss can strongly link neighboring collocation points to enable efficient training in sparse sample regimes, but its accuracy is restricted by the interpolation scheme. The proposed coupled-automatic-numerical differentiation framework, labeled as can-PINN, unifies the advantages of AD and ND, providing more robust and efficient training than AD-based PINNs, while further improving accuracy by up to 1-2 orders of magnitude relative to ND-based PINNs. For a proof-of-concept demonstration of this can-scheme to fluid dynamic problems, two numerical-inspired instantiations of can-PINN schemes for the convection and pressure gradient terms were derived to solve the incompressible Navier-Stokes (N-S) equations. The superior performance of can-PINNs is demonstrated on several challenging problems, including the flow mixing phenomena, lid driven flow in a cavity, and channel flow over a backward facing step. The results reveal that for challenging problems like these, can-PINNs can consistently achieve very good accuracy whereas conventional AD-based PINNs fail.