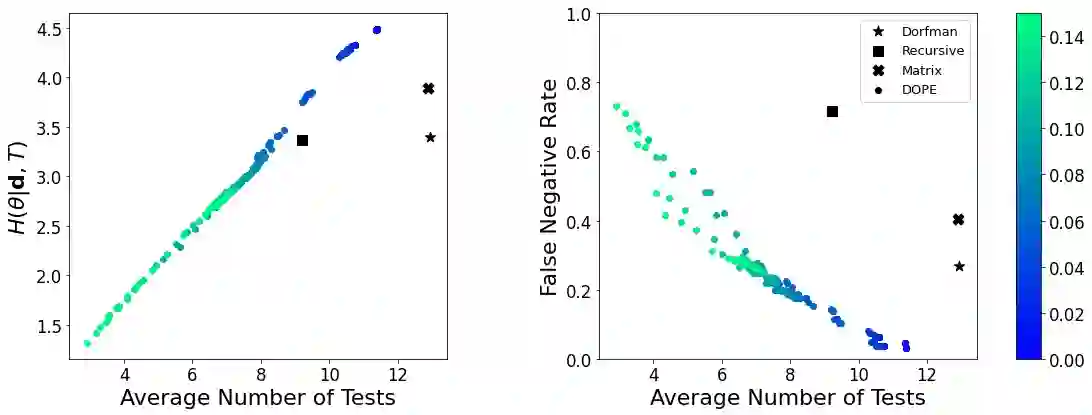
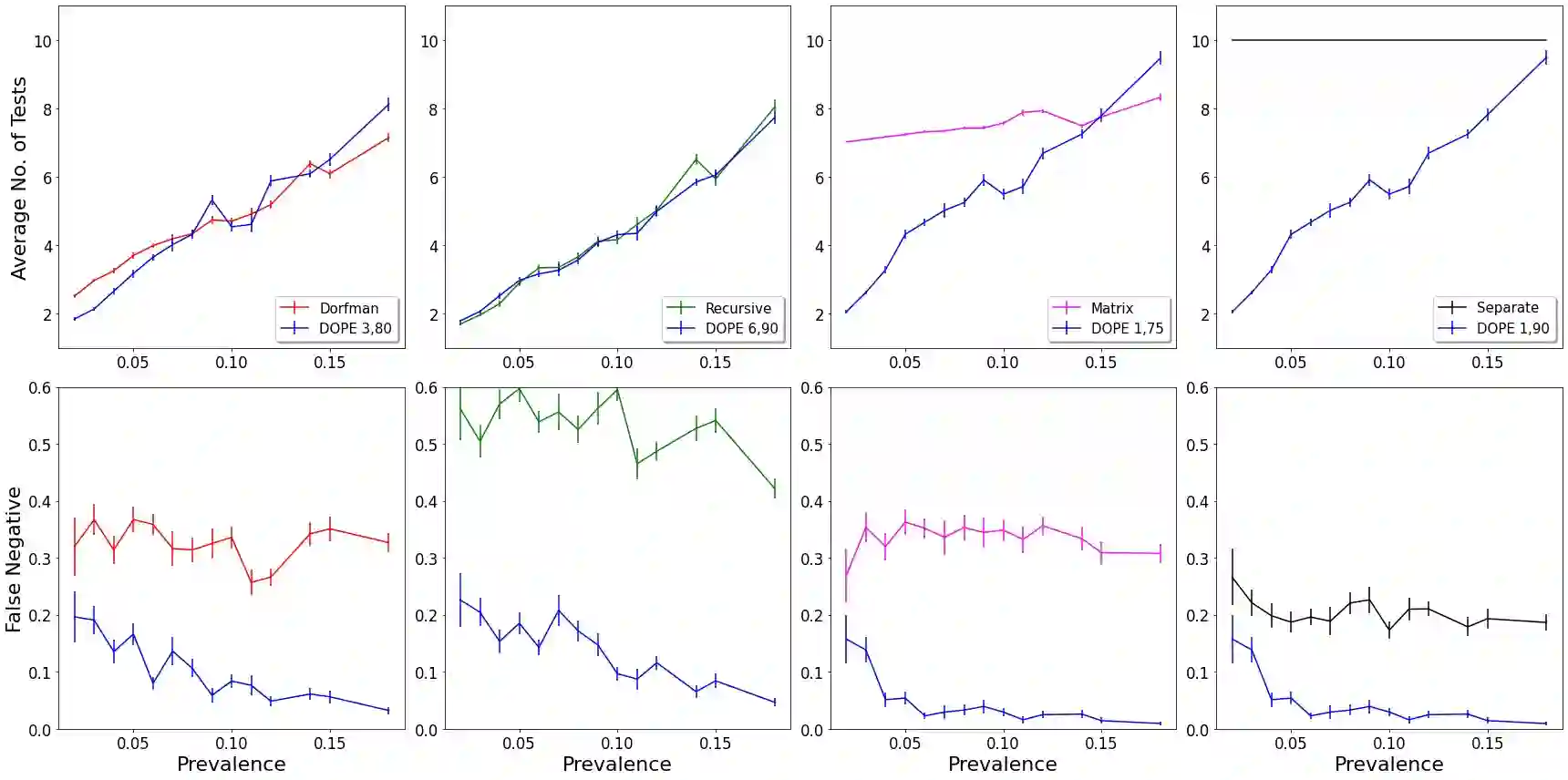
Testing individuals for the presence of severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2), the pathogen causing the coronavirus disease 2019 (COVID-19), is crucial for curtailing transmission chains. Moreover, rapidly testing many potentially infected individuals is often a limiting factor in controlling COVID-19 outbreaks. Hence, pooling strategies, wherein individuals are grouped and tested simultaneously, are employed. We present a novel pooling strategy that implements D-Optimal Pooling Experimental design (DOPE). DOPE defines optimal pooled tests as those maximizing the mutual information between data and infection states. We estimate said mutual information via Monte-Carlo sampling and employ a discrete optimization heuristic for maximizing it. DOPE outperforms common pooling strategies both in terms of lower error rates and fewer tests utilized. DOPE holds several additional advantages: it provides posterior distributions of the probability of infection, rather than only binary classification outcomes; it naturally incorporates prior information of infection probabilities and test error rates; and finally, it can be easily extended to include other, newly discovered information regarding COVID-19. Hence, we believe that implementation of Bayesian D-optimal experimental design holds a great promise for the efforts of combating COVID-19 and other future pandemics.
翻译:严重急性呼吸系统综合症冠状病毒2(SARS-COV-2)是2019年冠状病毒(COVID-19)的病原体,检测严重急性呼吸系统综合症冠状病毒2(SARS-COV-2)的存在,这是控制传播链的关键。此外,快速检测许多潜在感染者往往是控制COVID-19爆发的一个限制因素。因此,采用了同时对个人进行分组和测试的集合战略。我们提出了一个执行D-Oppimal 集合实验设计(DOPE)的新型集合战略。DOPE将最佳集合测试定义为通过蒙特-卡洛取样使数据和感染国之间相互信息最大化。我们估计说,相互信息是相互的,并使用离散的优化超常法来最大限度地增加这种信息。DOPE在低误差率和较少使用测试方面都优于共同集合战略。DOPE拥有一些额外优势:它提供了感染概率的后部分布,而不仅仅是二进分级分类结果;它自然将先前的感染概率和测试误率信息纳入;最后,它可以很容易将新发现的关于COVI-19的信息包括其他新发现的关于COVI-19的信息。因此,我们承诺今后进行伟大的实验设计。