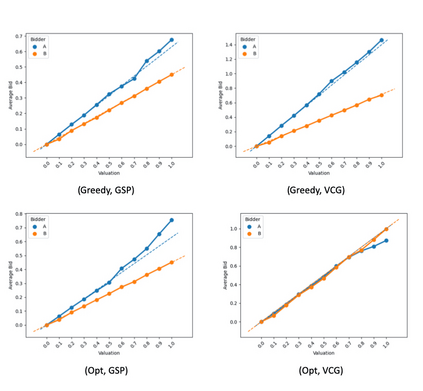
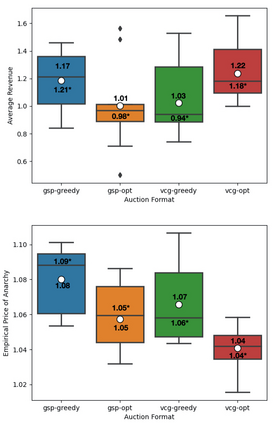
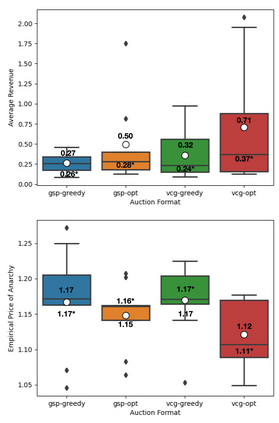
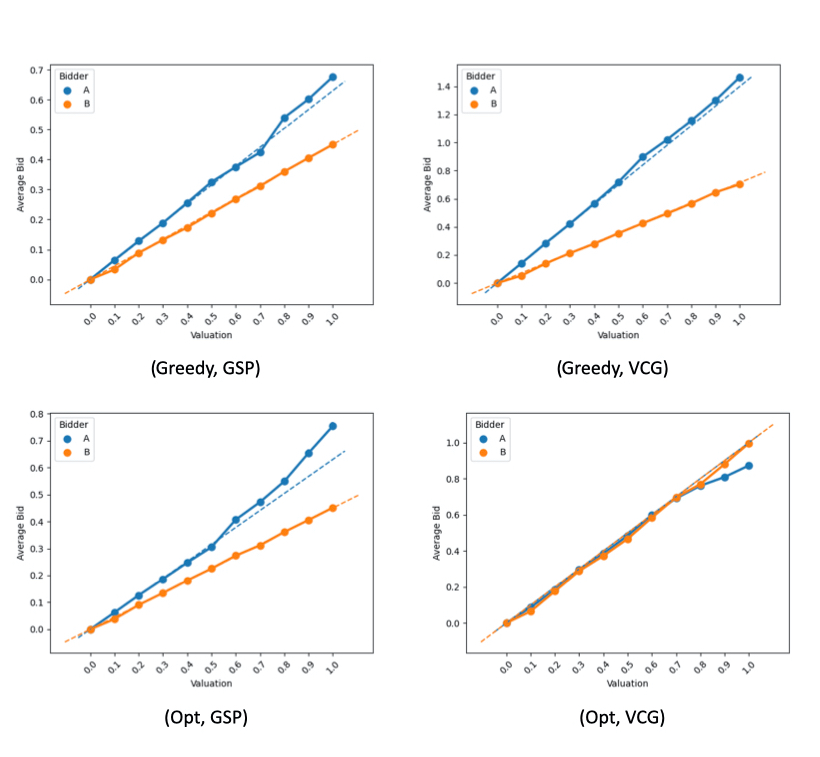
This paper studies equilibrium quality of semi-separable position auctions (known as the Ad Types setting) with greedy or optimal allocation combined with generalized second-price (GSP) or Vickrey-Clarke-Groves (VCG) pricing. We make three contributions: first, we give upper and lower bounds on the Price of Anarchy (PoA) for auctions which use greedy allocation with GSP pricing, greedy allocations with VCG pricing, and optimal allocation with GSP pricing. Second, we give Bayes-Nash equilibrium characterizations for two-player, two-slot instances (for all auction formats) and show that there exists both a revenue hierarchy and revenue equivalence across some formats. Finally, we use no-regret learning algorithms and bidding data from a large online advertising platform and no-regret learning algorithms to evaluate the performance of the mechanisms under semi-realistic conditions. For welfare, we find that the optimal-to-realized welfare ratio (an empirical PoA analogue) is broadly better than our upper bounds on PoA; For revenue, we find that the hierarchy in practice may sometimes agree with simple theory, but generally appears sensitive to the underlying distribution of bidder valuations.
翻译:本文对贪婪或最佳分配的半分离立场拍卖(称为 " 类型设置 " )的均衡质量进行了研究,这些拍卖具有贪婪或最佳分配,同时具有一般的第二价格(GSP)或Vickrey-Clarke-Groves(VCG)的定价。我们做出了三项贡献:首先,我们对使用贪婪分配的普惠制定价、贪婪分配的VCG定价和最佳分配的普惠制定价的拍卖(PoA)的无政府制价格进行上下限限制。第二,我们给双玩家、双档实例(所有拍卖形式)提供巴耶-纳什均衡的定性,并表明存在着收入等级和收入等同的某些格式。最后,我们用无政府学习的算法和从大型在线广告平台和无政府采购的数据来评估半现实条件下机制的绩效。关于福利,我们发现最佳到实现的福利比率(经验式PoA类比)比我们在PoA的上限要好得多;关于收入,我们发现,我们发现核心的等级分配方法有时似乎与敏感的估价方法一致。