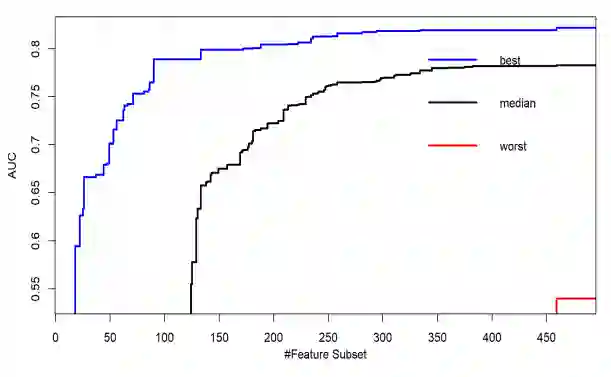
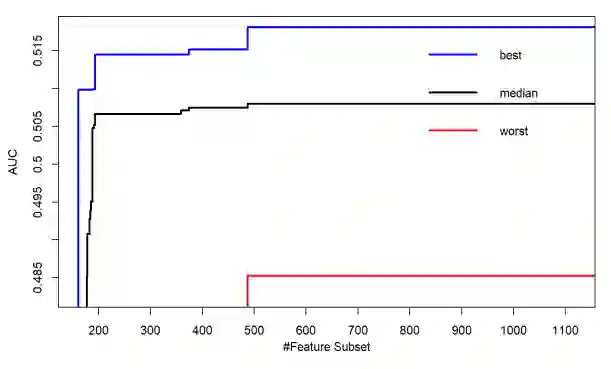
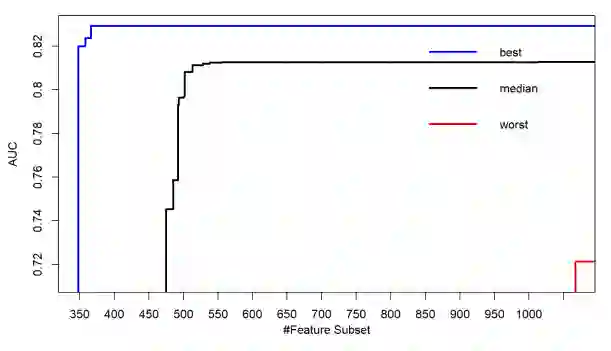
Feature subset selection (FSS) for classification is inherently a bi-objective optimization problem, where the task is to obtain a feature subset which yields the maximum possible area under the receiver operator characteristic curve (AUC) with minimum cardinality of the feature subset. In todays world, a humungous amount of data is generated in all activities of humans. To mine such voluminous data, which is often high-dimensional, there is a need to develop parallel and scalable frameworks. In the first-of-its-kind study, we propose and develop an iterative MapReduce-based framework for bi-objective evolutionary algorithms (EAs) based wrappers under Apache spark with the migration strategy. In order to accomplish this, we parallelized the non-dominated sorting based algorithms namely non dominated sorting algorithm (NSGA-II), and non-dominated sorting particle swarm optimization (NSPSO), also the decomposition-based algorithm, namely the multi-objective evolutionary algorithm based on decomposition (MOEA-D), and named them P-NSGA-II-IS, P-NSPSO-IS, P-MOEA-D-IS, respectively. We proposed a modified MOEA-D by incorporating the non-dominated sorting principle while parallelizing it. Throughout the study, AUC is computed by logistic regression (LR). We test the effectiveness of the proposed methodology on various datasets. It is noteworthy that the P-NSGA-II turns out to be statistically significant by being in the top 2 positions on most datasets. We also reported the empirical attainment plots, speed up analysis, and mean AUC obtained by the most repeated feature subset and the least cardinal feature subset with the highest AUC, and diversity analysis using hypervolume.
翻译:用于分类的奇特子选择( FSS) 本质上是一个双目标优化问题, 任务在于获得一个功能子集, 在接收器操作器特性曲线( AUC) 下产生最大可能的部域, 其特性子集为最小基点。 在当今世界, 人类的所有活动中都会生成大量数据。 要挖掘这种大量数据, 这些数据往往是高维的, 就需要开发平行和可缩放的框架。 在首项研究中, 我们提议并开发一个基于迭代的 MapRduce 框架, 用于在阿帕奇战略下基于双目标的演进算法(EAs) 包件(EAs) 。 为了实现这一点, 我们将非主控的排序算法( NSGA- II ) 和 基于非主控控控法的算法( P-MOEAs ), 使用最显著的A- MALS 的A- Silvacrial, 使用最显著的 A- MALS 和 MA- dal- dal- dal- real- recal- realialalal 。