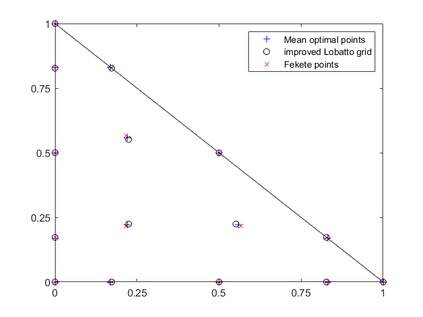
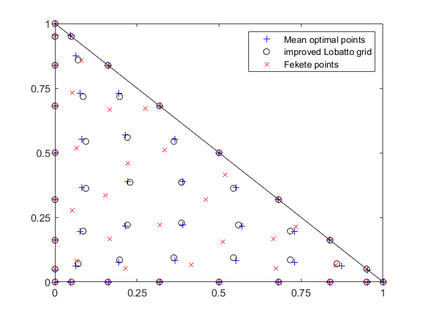
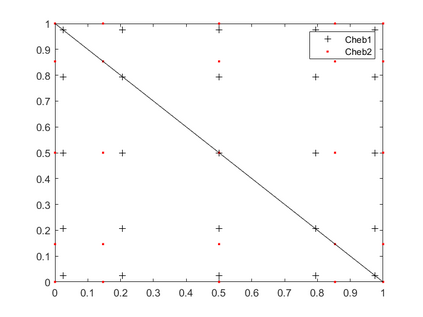
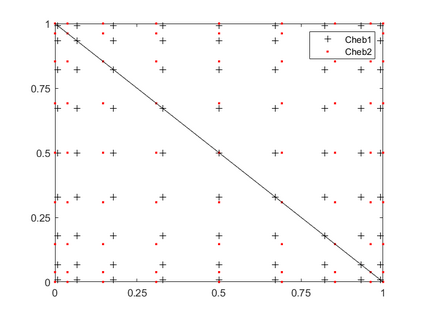
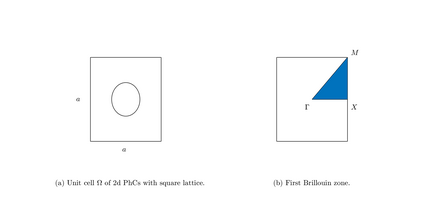
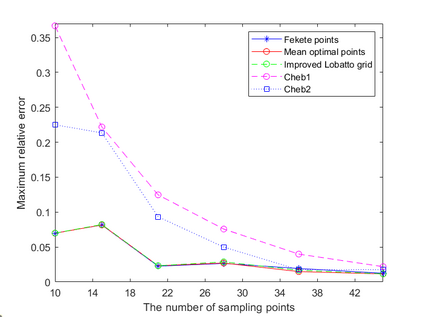
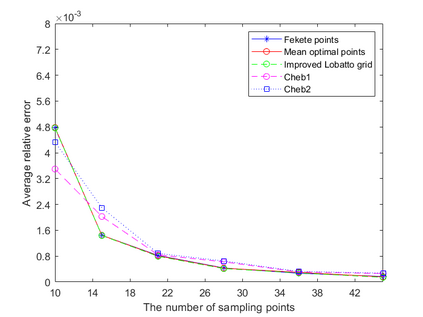
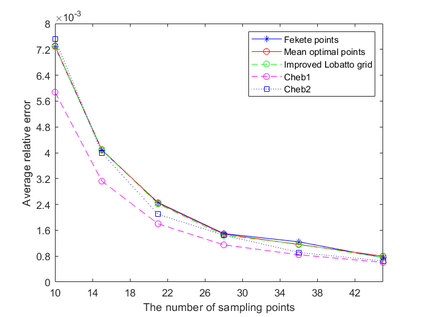
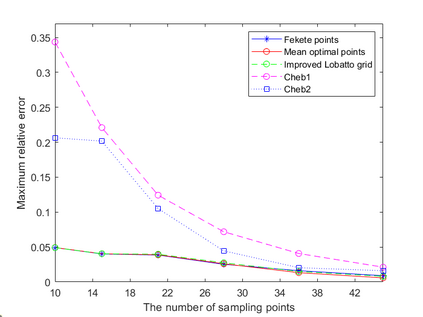
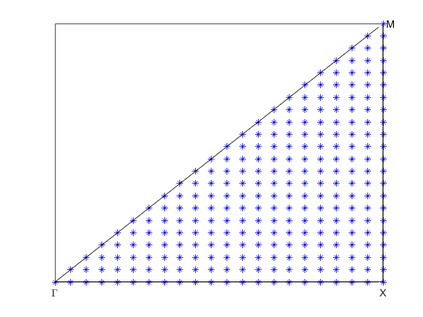
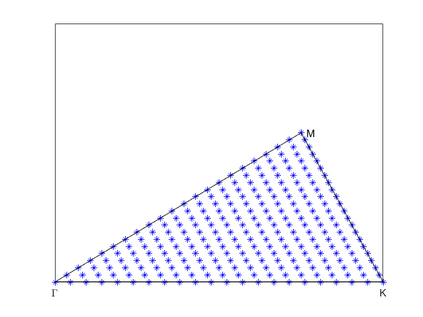
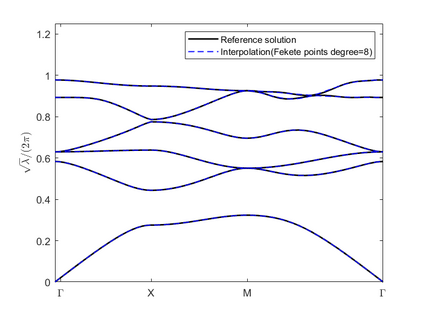
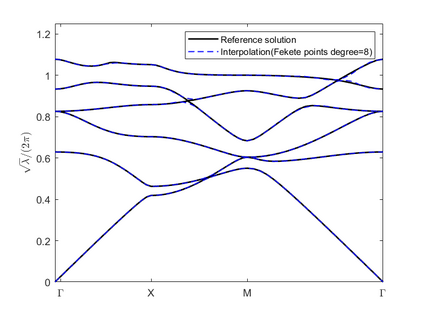
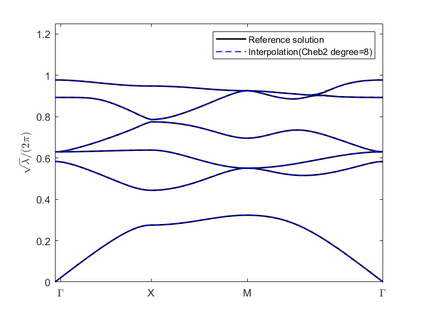
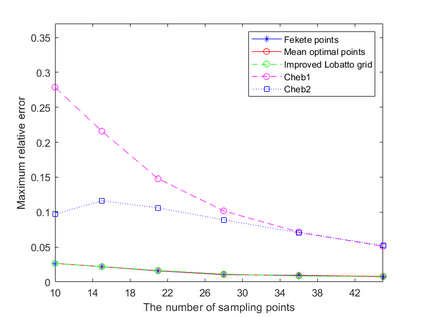
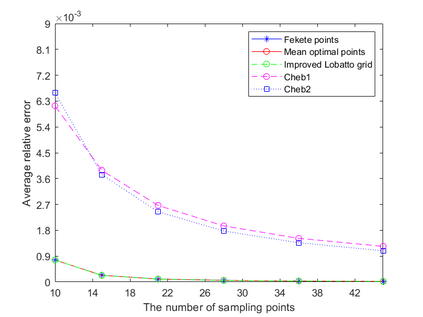
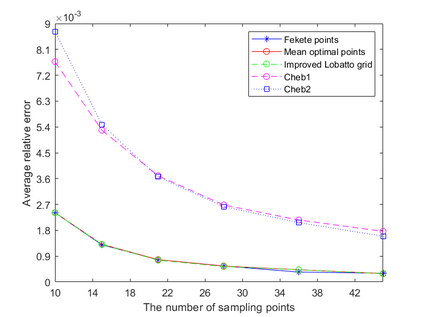
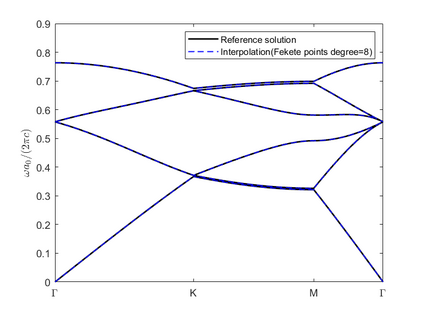
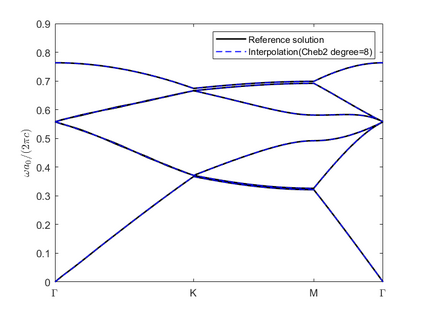
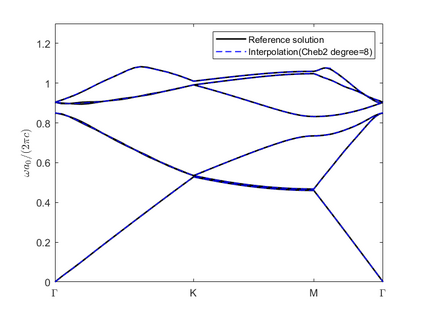
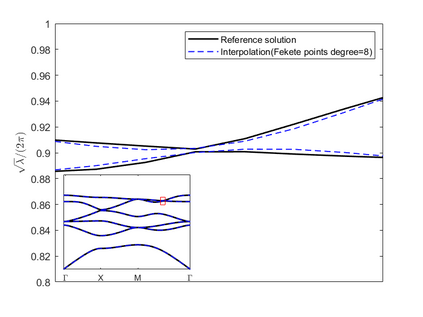
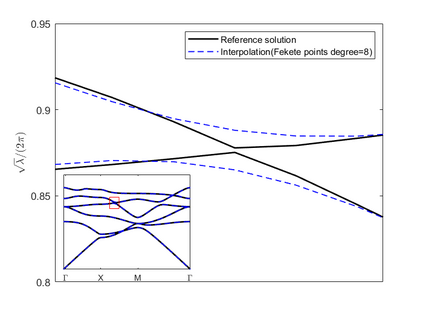
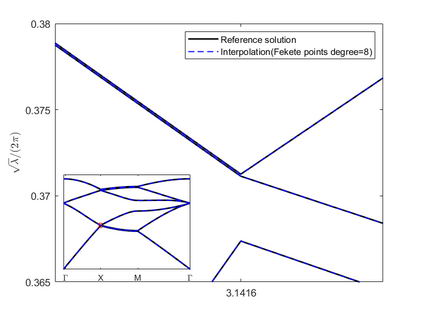
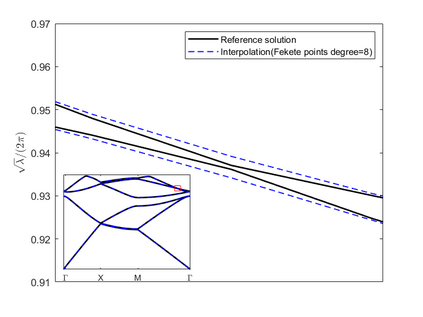
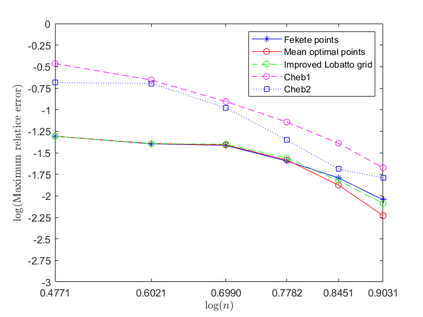
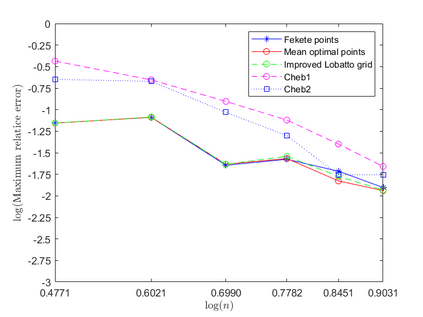
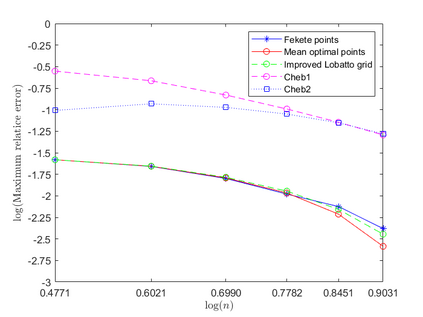
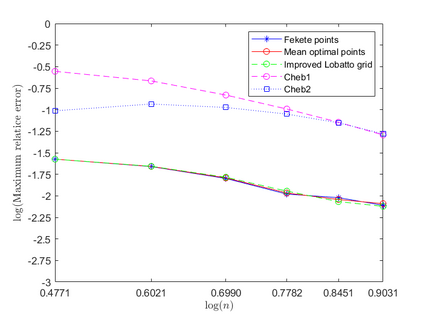
Dispersion relation reflects the dependence of wave frequency on its wave vector when the wave passes through certain material. It demonstrates the properties of this material and thus it is critical. However, dispersion relation reconstruction is very time consuming and expensive. To address this bottleneck, we propose in this paper an efficient dispersion relation reconstruction scheme based on global polynomial interpolation for the approximation of 2D photonic band functions. Our method relies on the fact that the band functions are piecewise analytic with respect to the wave vector in the first Brillouin zone. We utilize suitable sampling points in the first Brillouin zone at which we solve the eigenvalue problem involved in the band function calculation, and then employ Lagrange interpolation to approximate the band functions on the whole first Brillouin zone. Numerical results show that our proposed methods can significantly improve the computational efficiency.
翻译:色散关系反映了波在某种材料中通过时频率与波矢的依赖关系,展示了该材料的性质,因此至关重要。然而,色散关系的重建非常耗时且昂贵。为了解决这个瓶颈,本文提出了一种基于全局多项式插值的高效色散关系重建方案,用于近似二维光子带函数。我们的方法依赖于带函数在第一布里渊区中相对于波矢具有分段解析性的事实。我们在第一布里渊区中利用合适的采样点来解决涉及带函数计算的本征值问题,然后采用拉格朗日插值来逼近整个第一布里渊区内的带函数。数值结果表明,我们提出的方法可以显著提高计算效率。