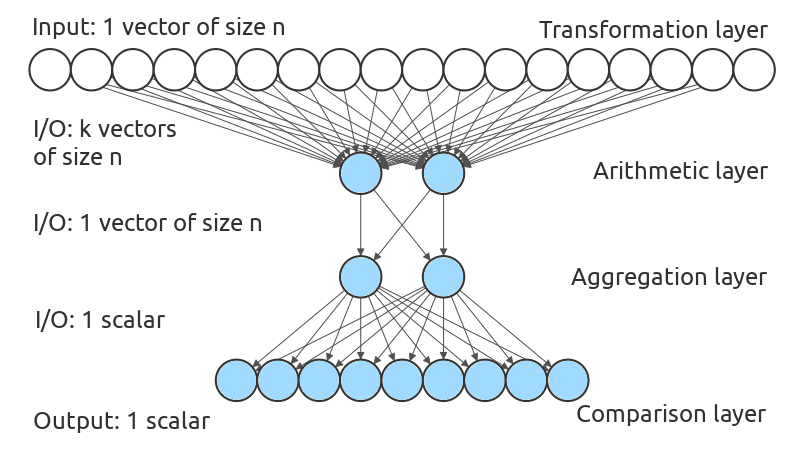
In Constraint Programming, constraints are usually represented as predicates allowing or forbidding combinations of values. However, some algorithms exploit a finer representation: error functions. Their usage comes with a price though: it makes problem modeling significantly harder. Here, we propose a method to automatically learn an error function corresponding to a constraint, given a function deciding if assignments are valid or not. This is, to the best of our knowledge, the first attempt to automatically learn error functions for hard constraints. Our method uses a variant of neural networks we named Interpretable Compositional Networks, allowing us to get interpretable results, unlike regular artificial neural networks. Experiments on 5 different constraints show that our system can learn functions that scale to high dimensions, and can learn fairly good functions over incomplete spaces.
翻译:在约束性编程中,制约通常被作为允许或禁止数值组合的前提。然而,有些算法利用了一个更精细的表达方式:错误函数。它们的使用带有一种价格:它使得问题模型的建模难度大得多。在这里,我们提出了一个方法来自动学习一个与限制相对应的错误函数,因为这个函数决定了任务是否有效。据我们所知,这是在硬性制约下自动学习错误函数的首个尝试。我们的方法使用一个我们命名为解释性组成网络的神经网络的变种,允许我们获得可解释的结果,而不像正常的人工神经网络。对5种不同的限制的实验显示,我们的系统可以学习高度尺寸的功能,并且可以在不完整的空间上学习相当好的功能。