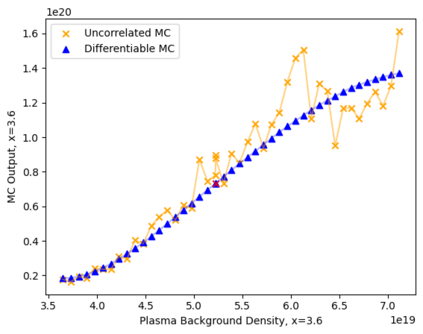
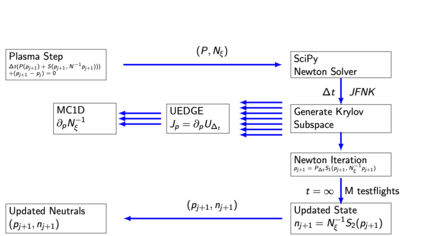
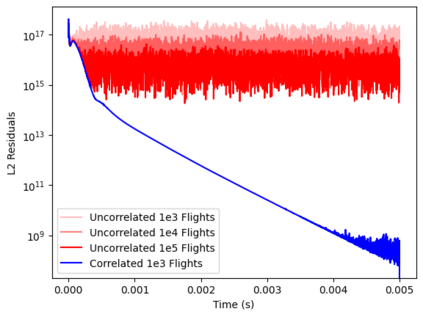
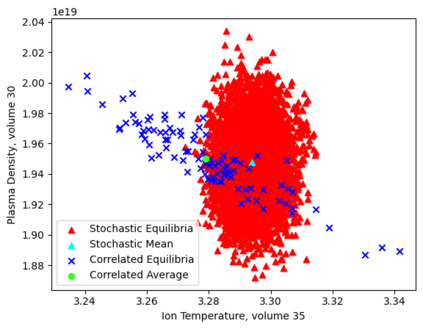
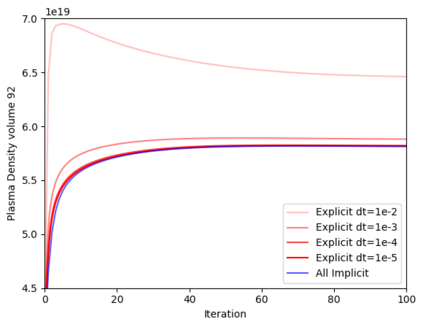
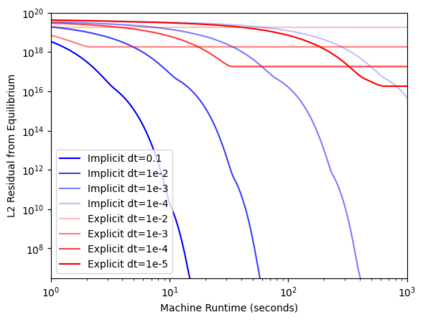
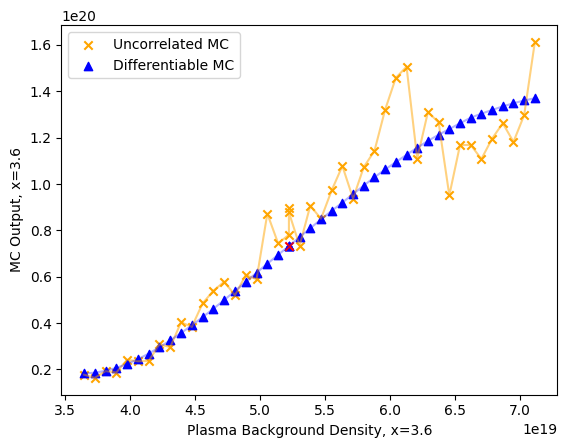
While boundary plasmas in present day tokamaks generally fall in a fluid regime, neutral species near the boundary often require kinetic models due to long mean-free-paths compared to characteristic spatial scales in the region. Monte-Carlo (MC) methods provide a complete, high-fidelity approach to solving kinetic models, and must be coupled to fluid plasma models to simulate the full plasma-neutrals system. The statistical nature of MC methods, however, prevents convergence of coupled fluid-kinetic simulations to an exact self-consistent steady-state. Moreover, this forces the use of explicit methods that can suffer from numerical errors and require huge computational resources. Correlated Monte-Carlo (CMC) methods are expected to alleviate these issues, but have historically enjoyed only mixed success. Here, a fully implicit method for coupled plasma-neutral systems is demonstrated in 1D using the UEDGE plasma code and a homemade CMC code. In particular, it is shown that ensuring the CMC method is a differentiable function of the background plasma is sufficient to employ a Jacobian-Free Newton-Krylov solver for implicit time steps. The convergence of the implicit coupling method is explored and compared with explicit coupling and uncorrelated methods. It is shown that ensuring differentiability by controlling random seeds in the MC is sufficient to achieve convergence, and that the use of implicit time-stepping methods has the potential for improved stability and runtimes over explicit coupling methods.
翻译:暂无翻译