Weak Galerkin methods based Morley elements on general polytopal partitions

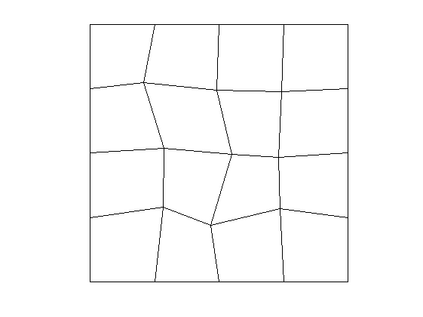
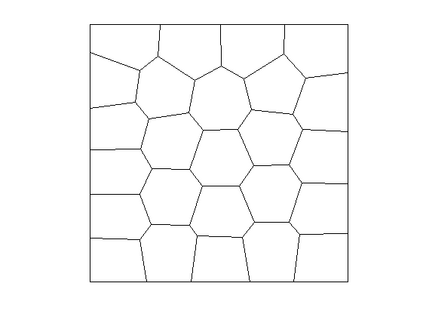
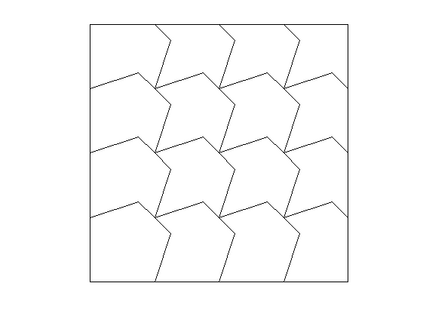
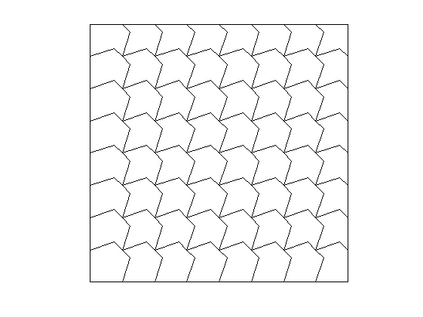
A new weak Galerkin method based on the weak tangential derivative and weak second order partial derivative is proposed to extend the well-known Morley element for the biharmonic equation from triangular elements to general polytopal elements. The Schur complement of the weak Galerkin scheme not only enjoys the same degrees of freedom as the Morley element on the triangular element but also extends the Morley element to any general polytopal element. The error estimates for the numerical approximation are established in the energy norm and the usual $L^2$ norms. Several numerical experiments are demonstrated to validate the theory developed in this article.