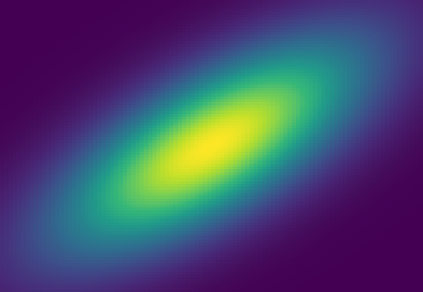
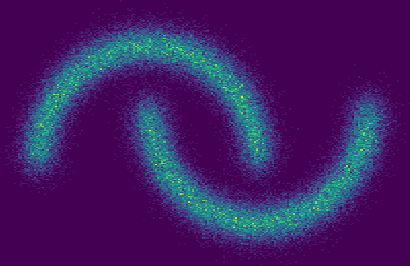
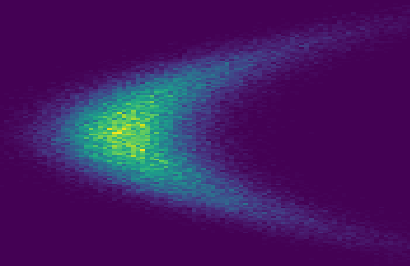
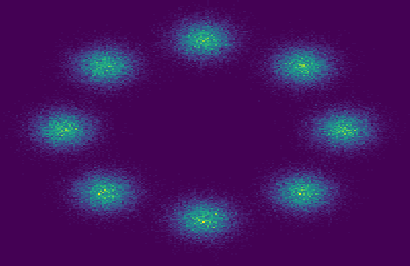
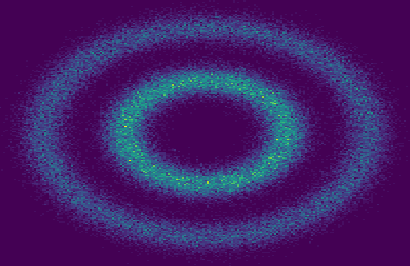
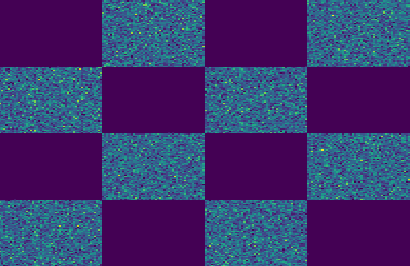
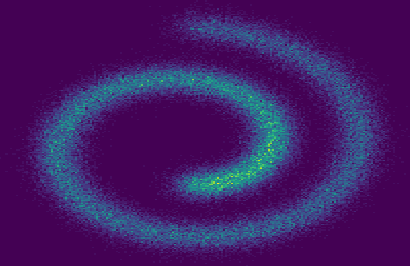
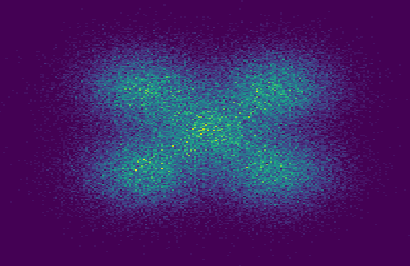
Triangular flows, also known as Kn\"{o}the-Rosenblatt measure couplings, comprise an important building block of normalizing flow models for generative modeling and density estimation, including popular autoregressive flow models such as real-valued non-volume preserving transformation models (Real NVP). We present statistical guarantees and sample complexity bounds for triangular flow statistical models. In particular, we establish the statistical consistency and the finite sample convergence rates of the Kullback-Leibler estimator of the Kn\"{o}the-Rosenblatt measure coupling using tools from empirical process theory. Our results highlight the anisotropic geometry of function classes at play in triangular flows, shed light on optimal coordinate ordering, and lead to statistical guarantees for Jacobian flows. We conduct numerical experiments on synthetic data to illustrate the practical implications of our theoretical findings.
翻译:三角流动,又称Kn\"{o}Rosenblatt测量组合,构成基因模型和密度估计的正常流动模型的重要组成部分,包括流行的自动递减流动模型,如实际价值的非量保存变异模型(Real NVP)。我们为三角流动统计模型提供了统计保障和样本复杂性界限。特别是,我们利用经验过程理论的工具,建立了Kn\"{o}the-Rosenblatt测量模型的Kullback-Leibel 测量器的统计一致性和有限样本合并率。我们的结果突显了三角流动中运行的功能类的厌异性几何学,说明了最佳协调顺序,并导致对Jacobian流动的统计保证。我们对合成数据进行了数字实验,以说明我们理论发现的实际影响。