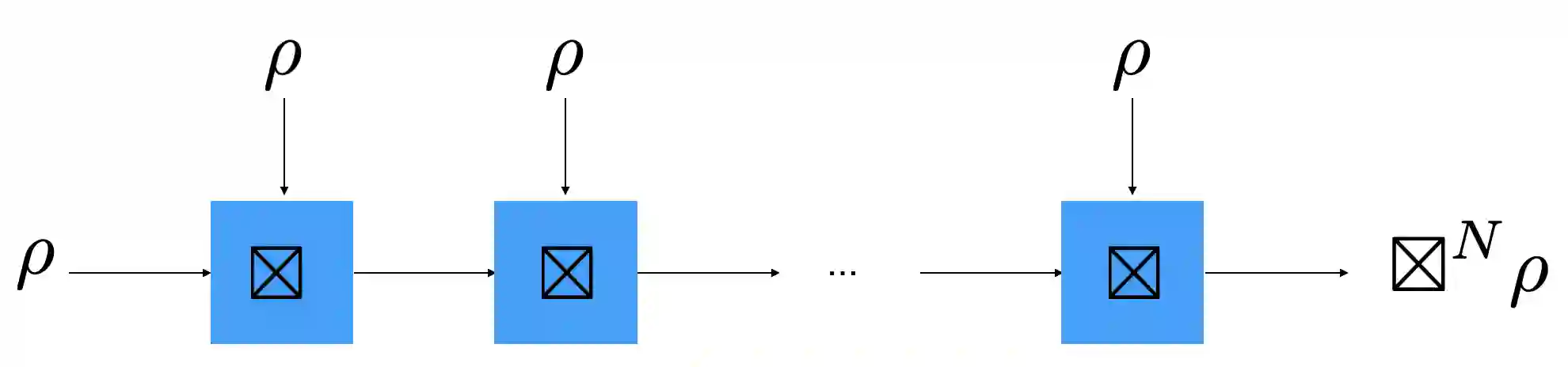
We establish an entropic, quantum central limit theorem and quantum inverse sumset theorem in discrete-variable quantum systems describing qudits or qubits. Both results are enabled by using our recently-discovered quantum convolution. We show that the exponential rate of convergence of the entropic central limit theorem is bounded by the magic gap. We also establish an ``quantum, entropic inverse sumset theorem,'' by introducing a quantum doubling constant. Furthermore, we introduce a ``quantum Ruzsa divergence'', and we pose a conjecture called ``convolutional strong subaddivity,'' which leads to the triangle inequality for the quantum Ruzsa divergence. A byproduct of this work is a magic measure to quantify the nonstabilizer nature of a state, based on the quantum Ruzsa divergence.
翻译:暂无翻译