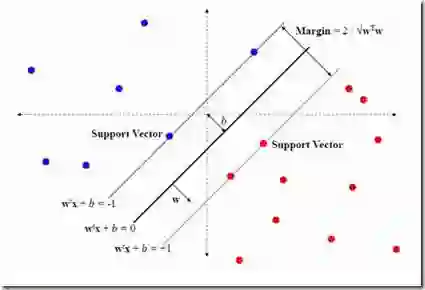
This work develops new results for stochastic approximation algorithms. The emphases are on treating algorithms and limits with discontinuities. The main ingredients include the use of differential inclusions, set-valued analysis, and non-smooth analysis, and stochastic differential inclusions. Under broad conditions, it is shown that a suitably scaled sequence of the iterates has a differential inclusion limit. In addition, it is shown for the first time that a centered and scaled sequence of the iterates converges weakly to a stochastic differential inclusion limit. The results are then used to treat several application examples including Markov decision process, Lasso algorithms, Pegasos algorithms, support vector machine classification, and learning. Some numerical demonstrations are also provided.
翻译:这项工作为随机近似算法开发了新的结果。 重点是处理算法和不连续限制。 主要成份包括使用差异包容、定值分析和非移动分析以及随机差异分析。 在广泛条件下, 显示迭代的合适比例序列具有差异包容限制。 此外, 首次显示迭代的中、 缩放序列与随机差异包容限制不匹配。 其结果被用来处理若干应用实例, 包括Markov 决策程序、 Lasso 算法、 Pegasos 算法、 支持矢量机分类和学习。 还提供一些数字演示。