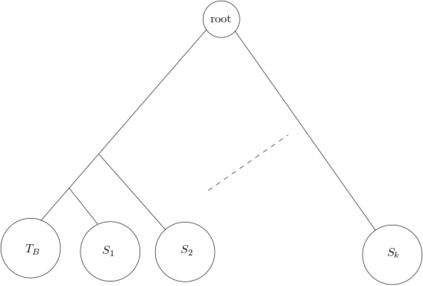
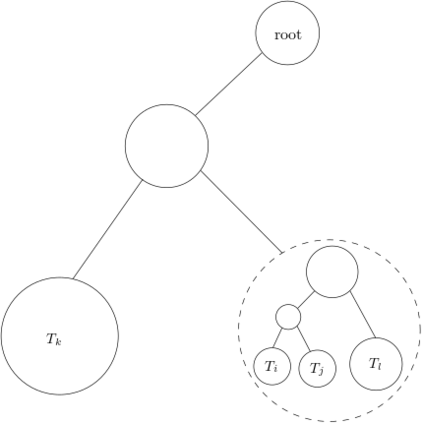
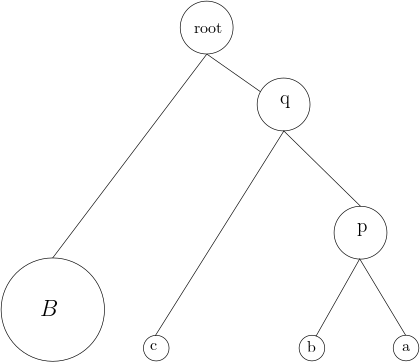
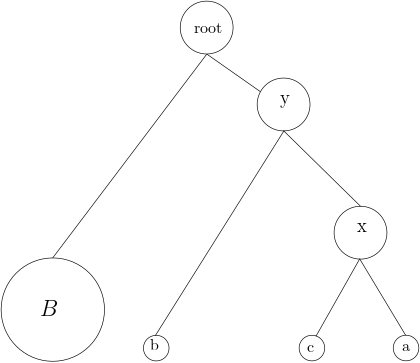
The problem of reconstructing evolutionary trees or phylogenies is of great interest in computational biology. A popular model for this problem assumes that we are given the set of leaves (current species) of an unknown binary tree and the results of `experiments' on triples of leaves (a,b,c), which return the pair with the deepest least common ancestor. If the tree is assumed to be an ultrametric (i.e., all root-leaf paths have the same length), the experiment can be equivalently seen to return the closest pair of leaves. In this model, efficient algorithms are known for tree reconstruction. In reality, since the data on which these `experiments' are run is itself generated by the stochastic process of evolution, these experiments are noisy. In all reasonable models of evolution, if the branches leading to the leaves in a triple separate from each other at common ancestors that are very close to each other in the tree, the result of the experiment should be close to uniformly random. Motivated by this, we consider a model where the noise on any triple is just dependent on the three pairwise distances (referred to as distance based noise). Our results are the following: 1. Suppose the length of every edge in the unknown tree is at least $\tilde{O}(\frac{1}{\sqrt n})$ fraction of the length of a root-leaf path. Then, we give an efficient algorithm to reconstruct the topology of the tree for a broad family of distance-based noise models. Further, we show that if the edges are asymptotically shorter, then topology reconstruction is information-theoretically impossible. 2. Further, for a specific distance-based noise model--which we refer to as the homogeneous noise model--we show that the edge weights can also be approximately reconstructed under the same quantitative lower bound on the edge lengths.
翻译:重建进化树或植物质的问题在计算生物学中引起了极大的兴趣。 这一问题流行的模式假设我们得到了未知的二进制树叶叶( 现有物种) 的一组有效算法 。 在现实中, 这些“ 实验” 的数据是由三叶叶叶叶( a, b, c) 的“ 实验” 的结果, 将两者的“ 实验” 与最不常见的祖先( a, b, c) 的“ 实验” 返回成一个超度( 即所有根叶路径都有相同的长度) 。 如果假设树的树叶系与树基中每棵树系非常接近, 实验的结果就等于返回最接近的一对叶叶叶。 在这个模型中, 高效的算法是树种之间的距离, 我们的底部是更低的“ ”, 我们的底部是更深的底部, 我们的底部是最深层的底部, 我们的底部是最深层的底部是最深处。