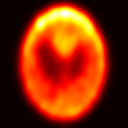
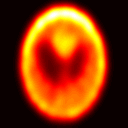
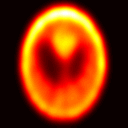
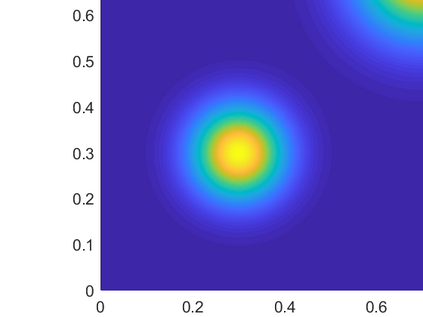
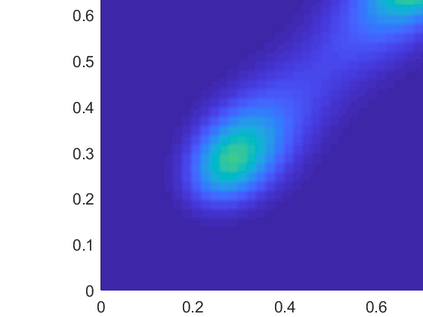
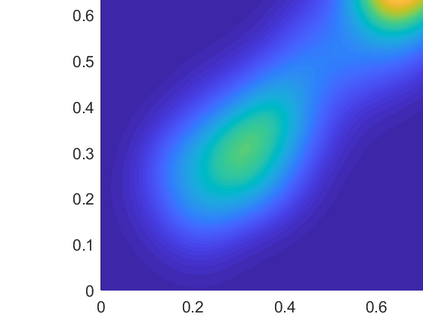
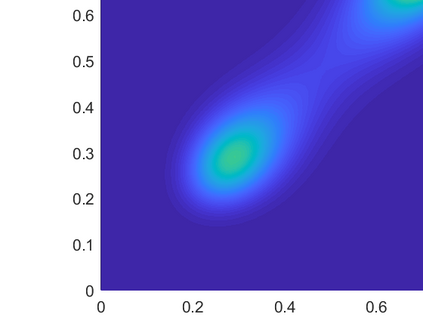
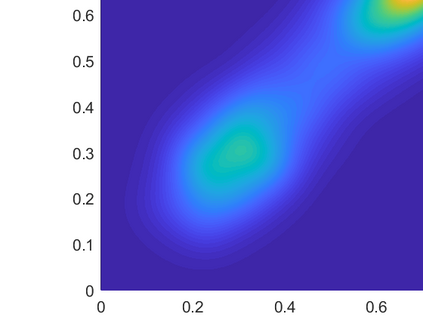
Fredholm integral equations of the first kind are the prototypical example of ill-posed linear inverse problems. They model, among other things, reconstruction of distorted noisy observations and indirect density estimation and also appear in instrumental variable regression. However, their numerical solution remains a challenging problem. Many techniques currently available require a preliminary discretization of the domain of the solution and make strong assumptions about its regularity. For example, the popular expectation maximization smoothing (EMS) scheme requires the assumption of piecewise constant solutions which is inappropriate for most applications. We propose here a novel particle method that circumvents these two issues. This algorithm can be thought of as a Monte Carlo approximation of the EMS scheme which not only performs an adaptive stochastic discretization of the domain but also results in smooth approximate solutions. We analyze the theoretical properties of the EMS iteration and of the corresponding particle algorithm. Compared to standard EMS, we show experimentally that our novel particle method provides state-of-the-art performance for realistic systems, including motion deblurring and reconstruction of cross-section images of the brain from positron emission tomography.
翻译:Fredholm 第一种整体方程式是典型的错误的线性反问题典型例子。 它们模型, 除其他外, 重建扭曲的噪音观测和间接密度估计, 并出现在工具性可变回归中。 然而, 其数字解决方案仍是一个挑战性的问题。 许多现有技术需要初步将解决方案的域分解, 并对其规律性做出强烈的假设。 例如, 大众期望最大化平滑( EMS) 方案要求假设对大多数应用来说不合适的小片常数解决方案。 我们在此建议一种绕过这两个问题的新型粒子方法。 这可以被认为是EMS 方案的蒙特卡洛近距离法, 不仅对域进行适应性分解, 而且还能产生光滑的近似解决方案。 我们分析了 EMS 和相应的粒子算法的理论属性。 与标准 EMS 相比, 我们实验性地显示, 我们的新粒子方法为现实的系统提供了最先进的状态性表现, 包括运动分流和将大脑的交叉图像从正向映射到映射法。