Generalizations to Corrections for the Effects of Measurement Error in Approximately Consistent Methodologies

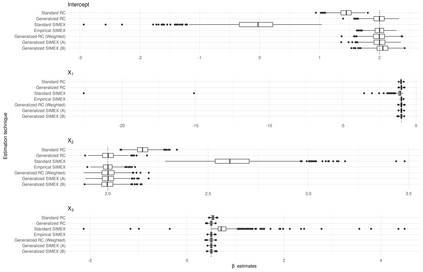
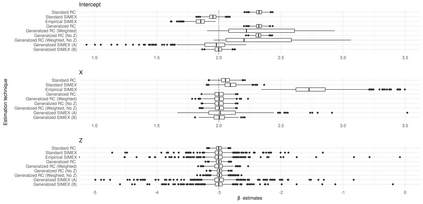
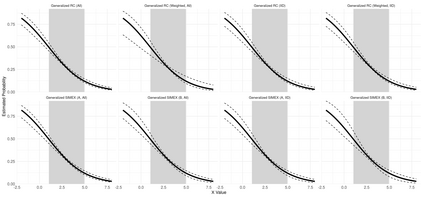
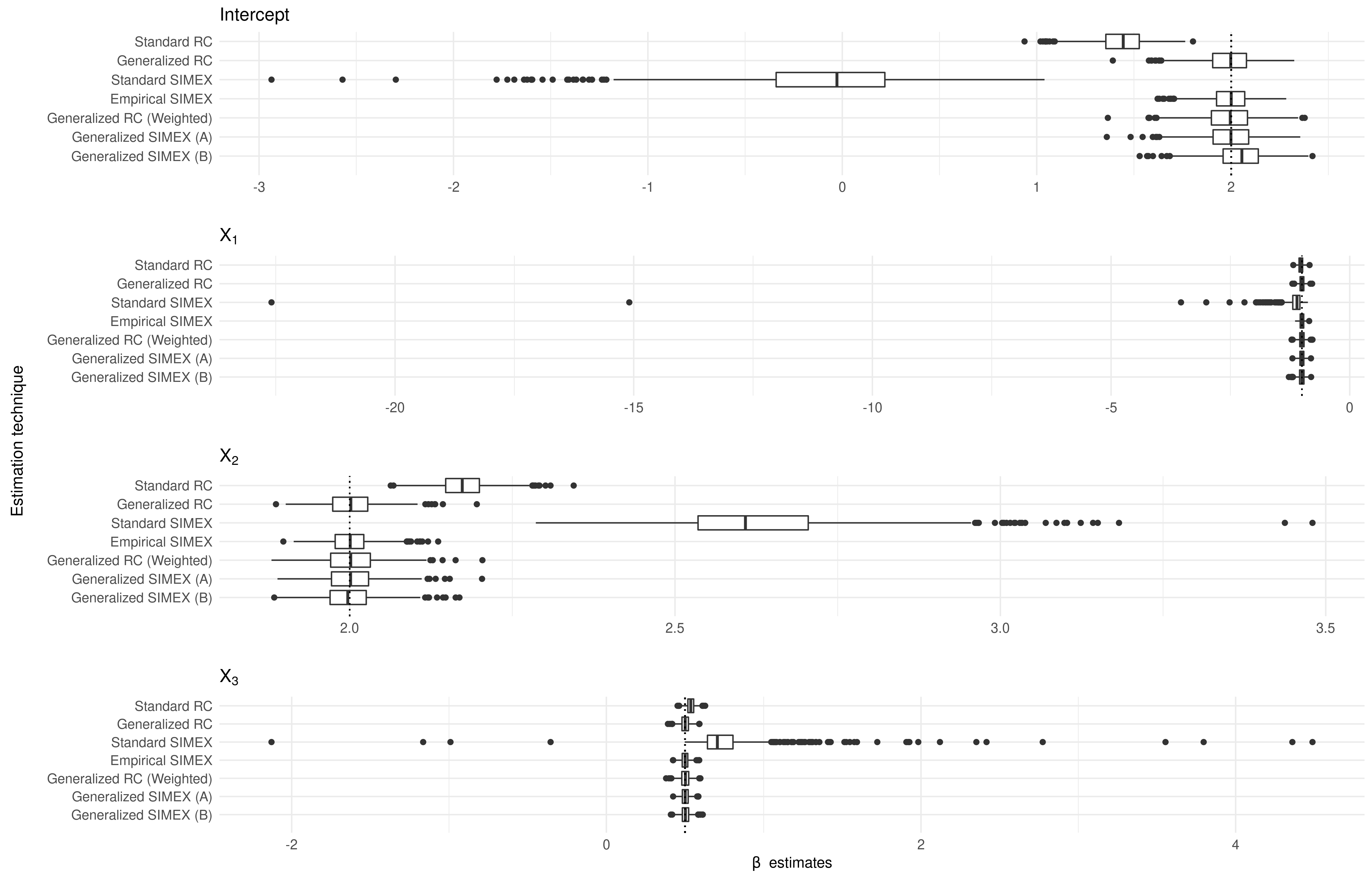
Measurement error is a pervasive issue which renders the results of an analysis unreliable. The measurement error literature contains numerous correction techniques, which can be broadly divided into those which aim to produce exactly consistent estimators, and those which are only approximately consistent. While consistency is a desirable property, it is typically attained only under specific model assumptions. Two approximately consistent techniques, regression calibration and simulation extrapolation, are used frequently in a wide variety of parametric and semiparametric settings. We generalize these corrections, relaxing assumptions placed on replicate measurements. Under regularity conditions, the estimators are shown to be asymptotically normal, with a sandwich estimator for the asymptotic variance. Through simulation, we demonstrate the improved performance of our estimators, over the standard techniques, when these assumptions are violated. We motivate these corrections using the Framingham Heart Study, and apply our generalized techniques to an analysis of these data.