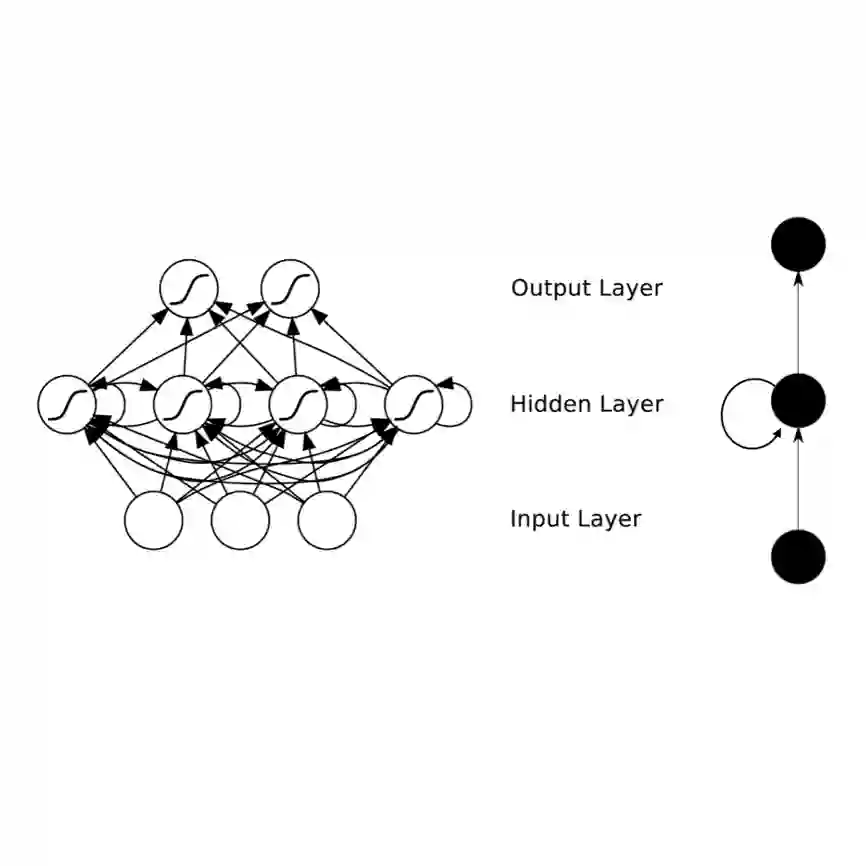
Recurrent Neural Network (RNN) is a fundamental structure in deep learning. Recently, some works study the training process of over-parameterized neural networks, and show that over-parameterized networks can learn functions in some notable concept classes with a provable generalization error bound. In this paper, we analyze the training and generalization for RNNs with random initialization, and provide the following improvements over recent works: 1) For a RNN with input sequence $x=(X_1,X_2,...,X_L)$, previous works study to learn functions that are summation of $f(\beta^T_lX_l)$ and require normalized conditions that $||X_l||\leq\epsilon$ with some very small $\epsilon$ depending on the complexity of $f$. In this paper, using detailed analysis about the neural tangent kernel matrix, we prove a generalization error bound to learn such functions without normalized conditions and show that some notable concept classes are learnable with the numbers of iterations and samples scaling almost-polynomially in the input length $L$. 2) Moreover, we prove a novel result to learn N-variables functions of input sequence with the form $f(\beta^T[X_{l_1},...,X_{l_N}])$, which do not belong to the "additive" concept class, i,e., the summation of function $f(X_l)$. And we show that when either $N$ or $l_0=\max(l_1,..,l_N)-\min(l_1,..,l_N)$ is small, $f(\beta^T[X_{l_1},...,X_{l_N}])$ will be learnable with the number iterations and samples scaling almost-polynomially in the input length $L$.
翻译:经常性神经网络( RNNN) 是深层学习的基本结构 。 最近, 一些工作研究过量参数化神经网络的培训过程, 并显示超度化网络可以在某些值得注意的概念类中学习函数, 并附带可验证的通用错误 。 在本文中, 我们分析随机初始化的 RNN 的培训和概括化, 并提供与最近作品相比的以下改进 :1 对于输入序列 $= (X_ 1, X_ 2,..., X_L) 的 RNN (NNNNN), 先前的工作研究, 以学习总计值为$( teta_T_ lX) 的函数, 并且要求标准化条件 $_\\ lQ_ 美元( leql), 取决于 $1 的复杂程度 。 在本文中, 详细分析 nurorg 内嵌入的矩阵, 我们证明在不规范的条件下学习这种函数是一般性的, 显示某些值得注意的概念类级, 和样本缩数是 $_xx 。