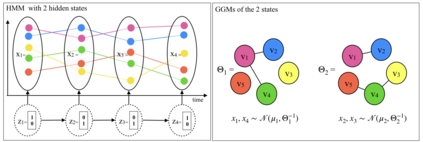
Multivariate time series analysis is becoming an integral part of data analysis pipelines. Understanding the individual time point connections between covariates as well as how these connections change in time is non-trivial. To this aim, we propose a novel method that leverages on Hidden Markov Models and Gaussian Graphical Models -- Time Adaptive Gaussian Model (TAGM). Our model is a generalization of state-of-the-art methods for the inference of temporal graphical models, its formulation leverages on both aspects of these models providing better results than current methods. In particular,it performs pattern recognition by clustering data points in time; and, it finds probabilistic (and possibly causal) relationships among the observed variables. Compared to current methods for temporal network inference, it reduces the basic assumptions while still showing good inference performances.
翻译:多变量时间序列分析正在成为数据分析管道的一个组成部分。 理解共变量之间的单个时间点联系以及这些联系在时间上的变化如何是非三重的。 为此,我们提出一种新的方法,利用隐藏的马尔科夫模型和高西亚图形模型 -- -- 时间适应性高斯模型。 我们的模型是时间图形模型推断最新方法的概括化。 模型的拟订利用了这两个模型的两部分,提供了比当前方法更好的结果。 特别是,它按时间数据点进行模式识别;它发现所观察到变量之间的概率(可能也是因果)关系。 与目前的时间网络推论方法相比,它减少了基本假设,同时仍然显示良好的推理性。