Potential Singularity of the Axisymmetric Euler Equations with $C^α$ Initial Vorticity for A Large Range of $α$. Part I: the $3$-Dimensional Case

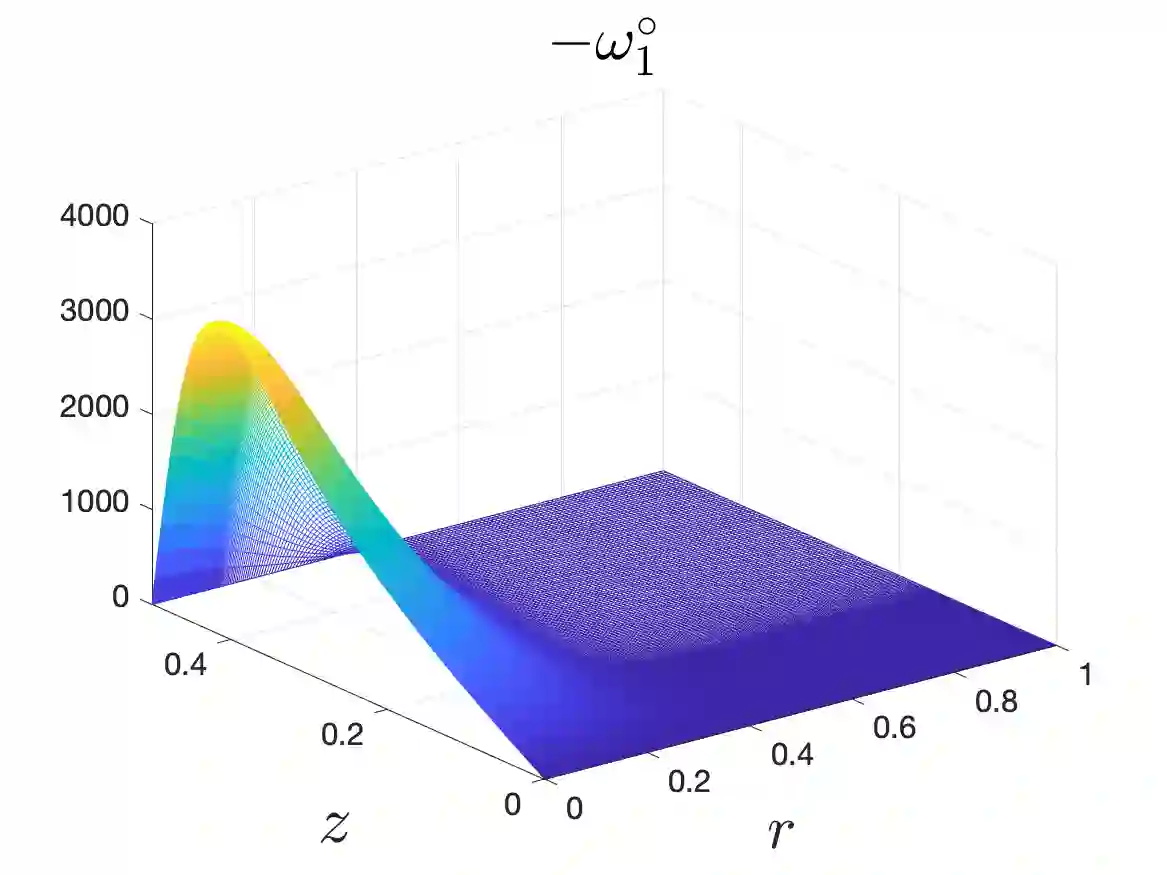
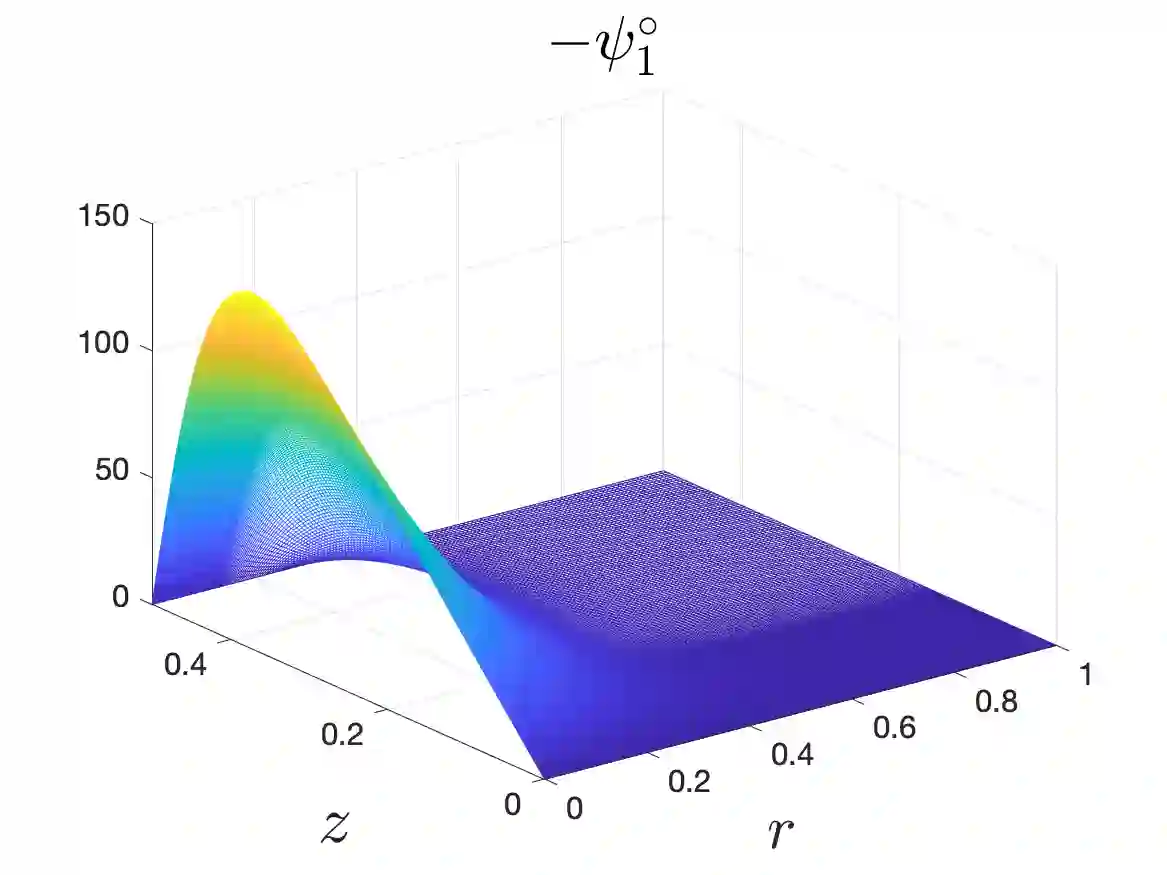
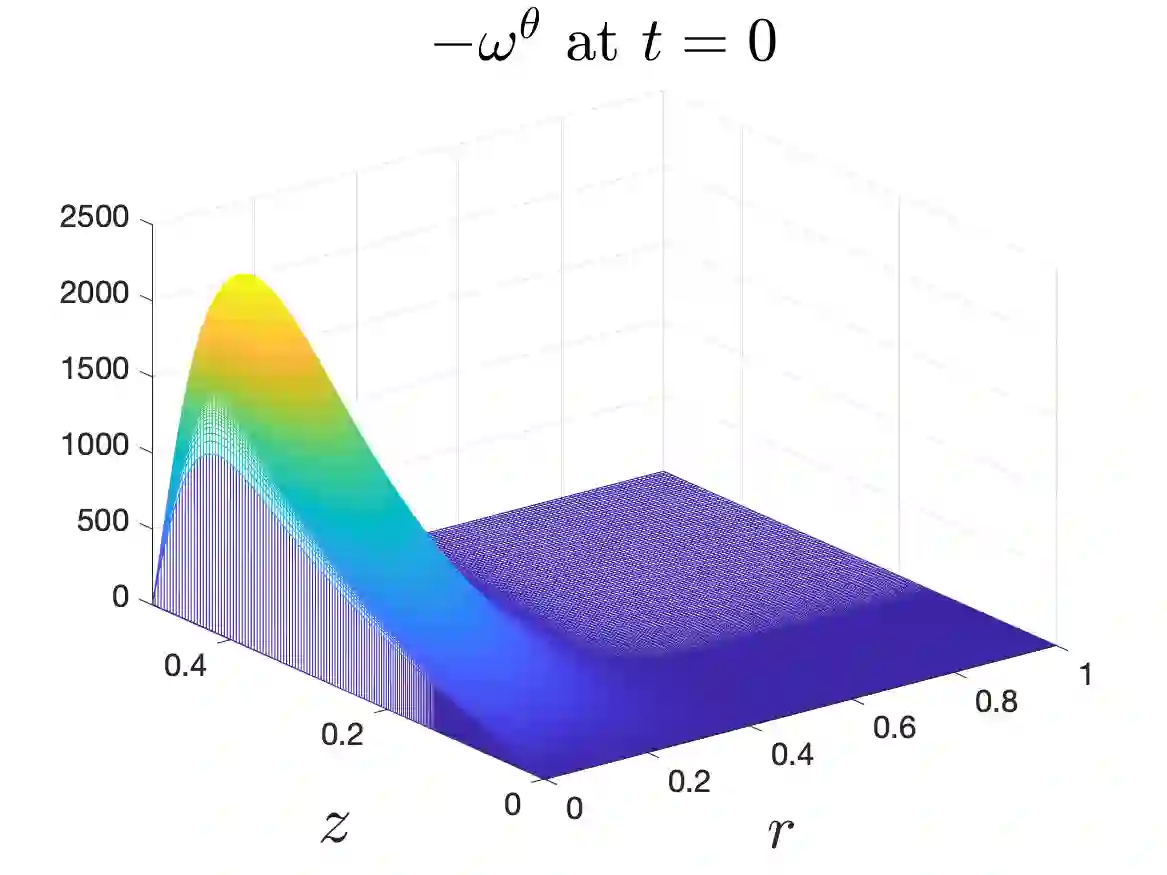
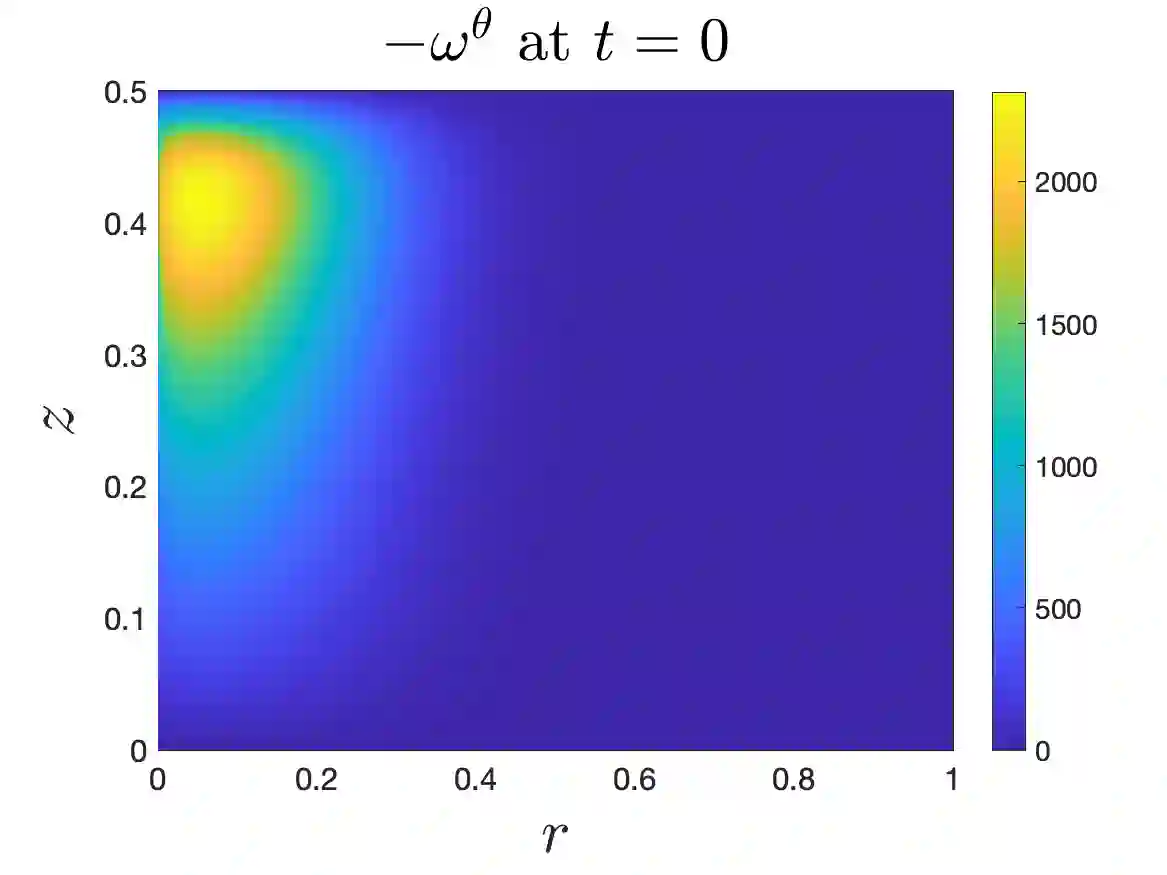
In Part I of our sequence of 2 papers, we provide numerical evidence for a potential finite-time self-similar singularity of the 3D axisymmetric Euler equations with no swirl and with $C^\alpha$ initial vorticity for a large range of $\alpha$. We employ an adaptive mesh method using a highly effective mesh to resolve the potential singularity sufficiently close to the potential blow-up time. Resolution study shows that our numerical method is at least second-order accurate. Scaling analysis and the dynamic rescaling formulation are presented to quantitatively study the scaling properties of the potential singularity. We demonstrate that this potential blow-up is stable with respect to the perturbation of initial data. Our study shows that the 3D Euler equations with our initial data develop finite-time blow-up when the H\"older exponent $\alpha$ is smaller than some critical value $\alpha^*$. By properly rescaling the initial data in the $z$-axis, this upper bound for potential blow-up $\alpha^*$ can asymptotically approach $1/3$. Compared with Elgindi's blow-up result in a similar setting \cite{elgindi2021finite}, our potential blow-up scenario has a different H\"older continuity property in the initial data and the scaling properties of the two initial data are also quite different.