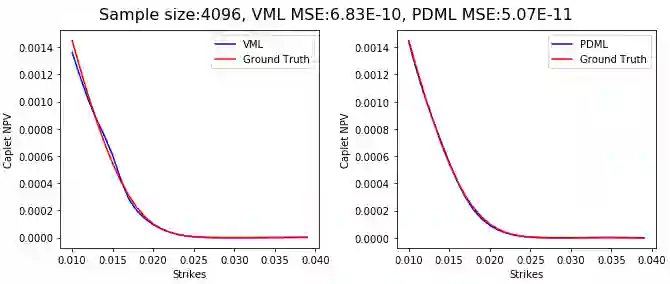
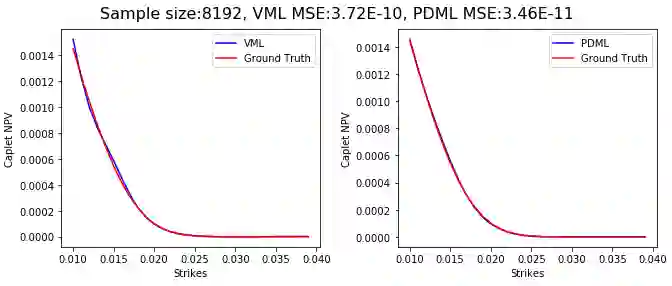
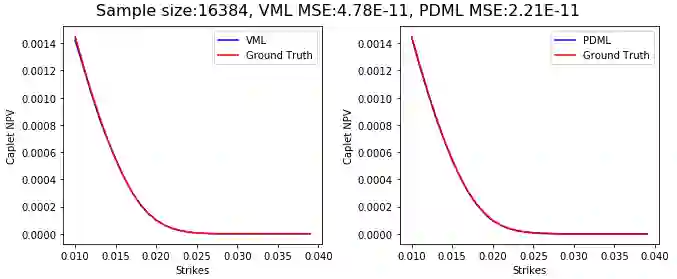
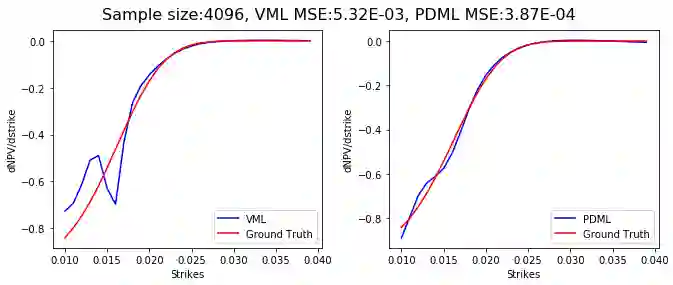
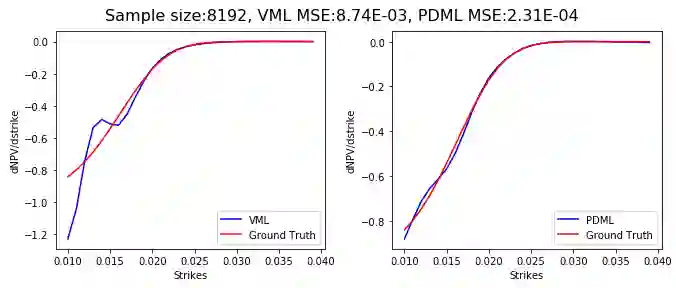
Differential machine learning (DML) is a recently proposed technique that uses samplewise state derivatives to regularize least square fits to learn conditional expectations of functionals of stochastic processes as functions of state variables. Exploiting the derivative information leads to fewer samples than a vanilla ML approach for the same level of precision. This paper extends the methodology to parametric problems where the processes and functionals also depend on model and contract parameters, respectively. In addition, we propose adaptive parameter sampling to improve relative accuracy when the functionals have different magnitudes for different parameter sets. For calibration, we construct pricing surrogates for calibration instruments and optimize over them globally. We discuss strategies for robust calibration. We demonstrate the usefulness of our methodology on one-factor Cheyette models with benchmark rate volatility specification with an extra stochastic volatility factor on (two-curve) caplet prices at different strikes and maturities, first for parametric pricing, and then by calibrating to a given caplet volatility surface. To allow convenient and efficient simulation of processes and functionals and in particular the corresponding computation of samplewise derivatives, we propose to specify the processes and functionals in a low-code way close to mathematical notation which is then used to generate efficient computation of the functionals and derivatives in TensorFlow.
翻译:差异机器学习(DML)是最近提出的一种技术,它使用抽样状态衍生物来规范最不适的参数,学习对随机过程功能的有条件期望,作为国家变量的功能。利用衍生物信息导致的样本少于香草 ML 方法,精确度相同。本文将方法扩大到参数问题,其中流程和功能也分别取决于模型和合同参数。此外,我们提出适应性参数抽样,以提高功能不同参数组不同大小时的相对准确性。在校准方面,我们为校准仪器建造代价替代物,并优化全球范围。我们讨论强力校准战略。我们用具有基准率波动规格的单片Cheyette模型展示了我们的方法的效用,在(双曲线)不同罢工和成熟度的封顶价价格上,先是偏差定价,然后对给定的峰值波动表表面进行校准。为了方便和高效模拟过程和功能功能,特别是精确地计算样品衍生物。我们提议,在(两曲线)下,在(双曲线)卡价格上,在(双曲线)不同情况下,用高效的模型计算方法,然后是高效的数学计算。