Analytical Discovery of Manifold with Machine Learning

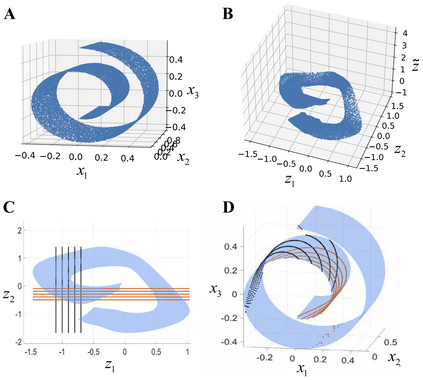
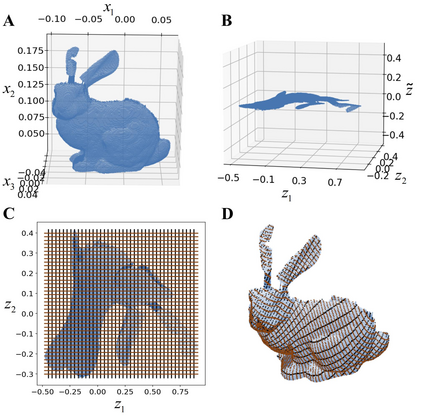
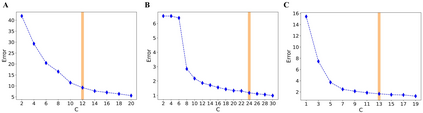
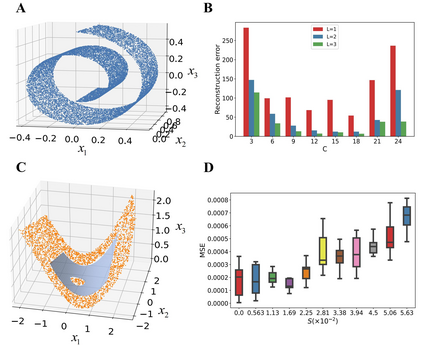
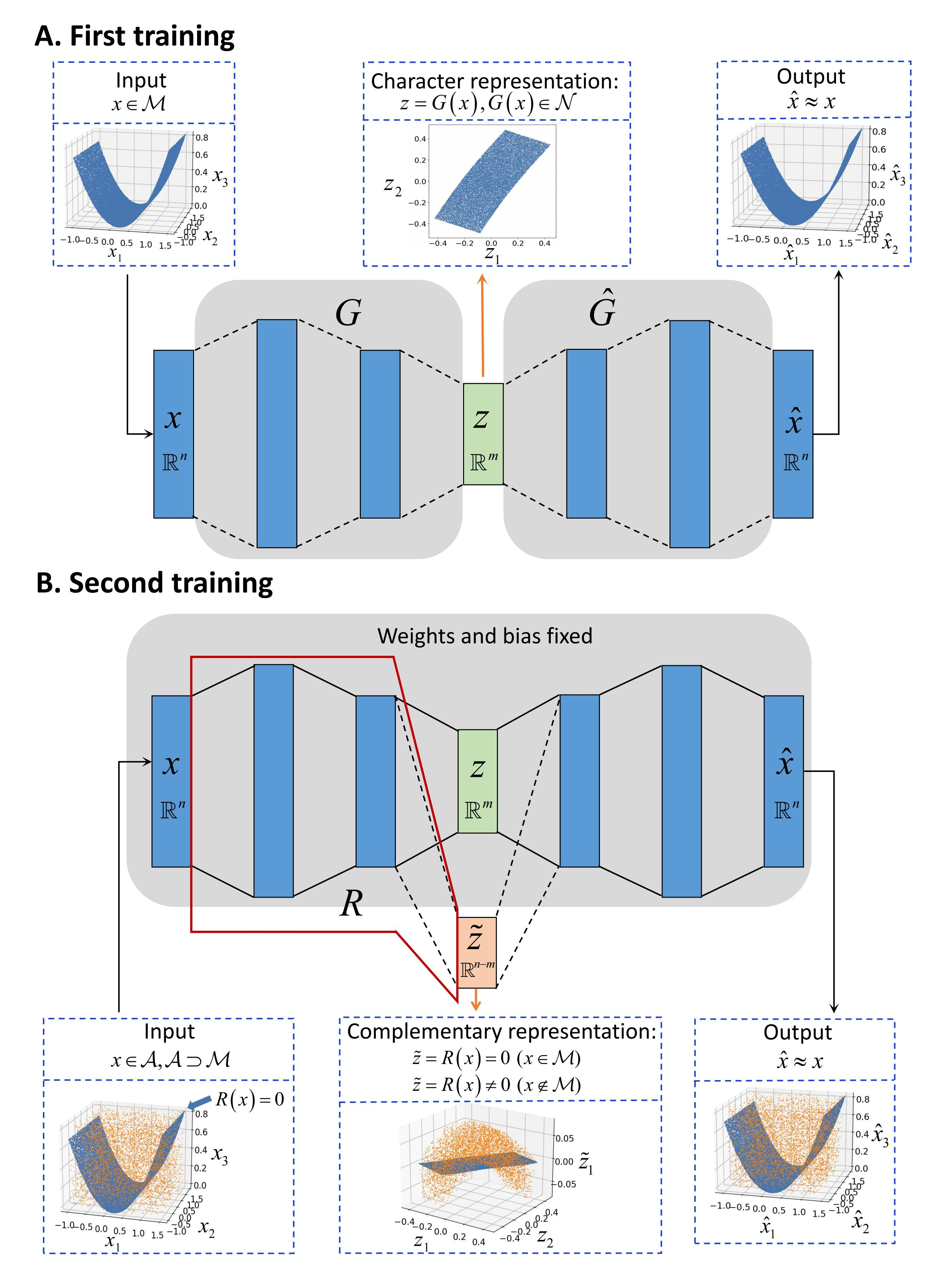
Understanding low-dimensional structures within high-dimensional data is crucial for visualization, interpretation, and denoising in complex datasets. Despite the advancements in manifold learning techniques, key challenges-such as limited global insight and the lack of interpretable analytical descriptions-remain unresolved. In this work, we introduce a novel framework, GAMLA (Global Analytical Manifold Learning using Auto-encoding). GAMLA employs a two-round training process within an auto-encoding framework to derive both character and complementary representations for the underlying manifold. With the character representation, the manifold is represented by a parametric function which unfold the manifold to provide a global coordinate. While with the complementary representation, an approximate explicit manifold description is developed, offering a global and analytical representation of smooth manifolds underlying high-dimensional datasets. This enables the analytical derivation of geometric properties such as curvature and normal vectors. Moreover, we find the two representations together decompose the whole latent space and can thus characterize the local spatial structure surrounding the manifold, proving particularly effective in anomaly detection and categorization. Through extensive experiments on benchmark datasets and real-world applications, GAMLA demonstrates its ability to achieve computational efficiency and interpretability while providing precise geometric and structural insights. This framework bridges the gap between data-driven manifold learning and analytical geometry, presenting a versatile tool for exploring the intrinsic properties of complex data sets.