Time Series Anomaly Detection by Cumulative Radon Features

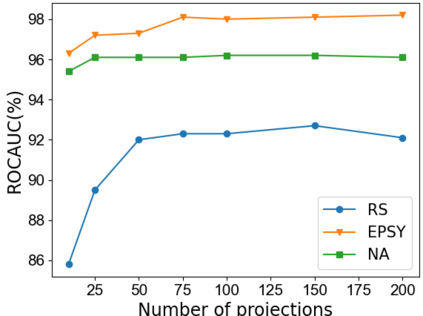
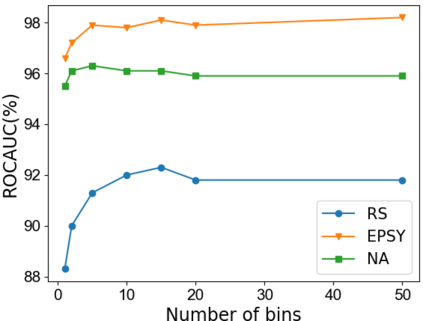
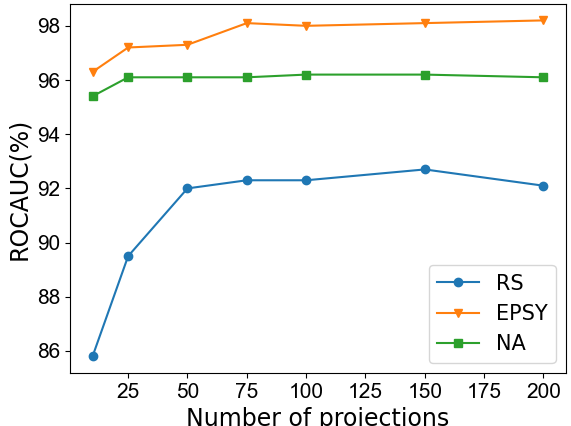
Detecting anomalous time series is key for scientific, medical and industrial tasks, but is challenging due to its inherent unsupervised nature. In recent years, progress has been made on this task by learning increasingly more complex features, often using deep neural networks. In this work, we argue that shallow features suffice when combined with distribution distance measures. Our approach models each time series as a high dimensional empirical distribution of features, where each time-point constitutes a single sample. Modeling the distance between a test time series and the normal training set therefore requires efficiently measuring the distance between multivariate probability distributions. We show that by parameterizing each time series using cumulative Radon features, we are able to efficiently and effectively model the distribution of normal time series. Our theoretically grounded but simple-to-implement approach is evaluated on multiple datasets and shown to achieve better results than established, classical methods as well as complex, state-of-the-art deep learning methods. Code is provided.