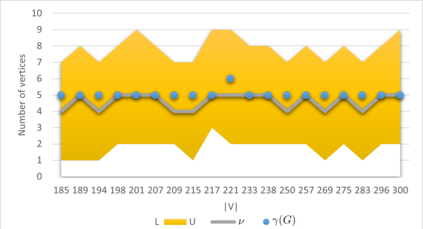
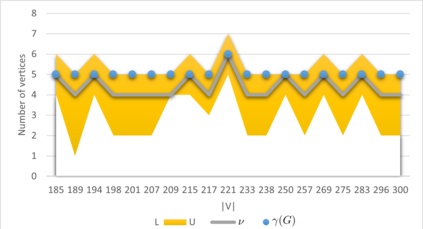
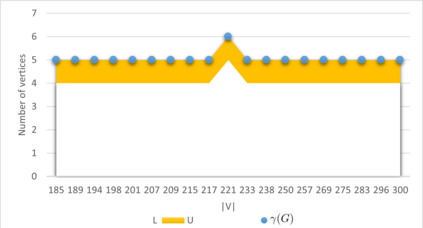
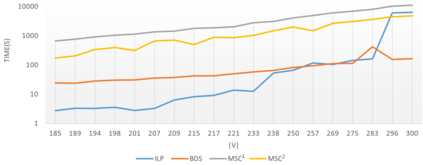
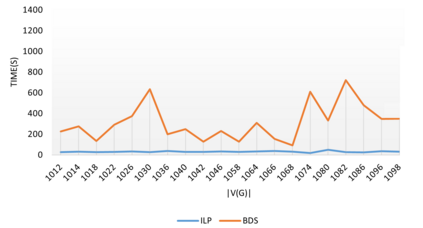
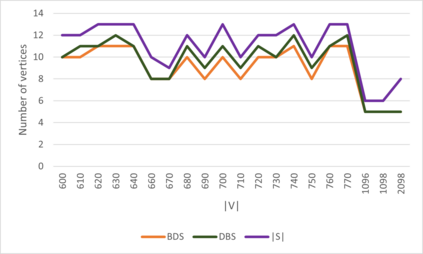
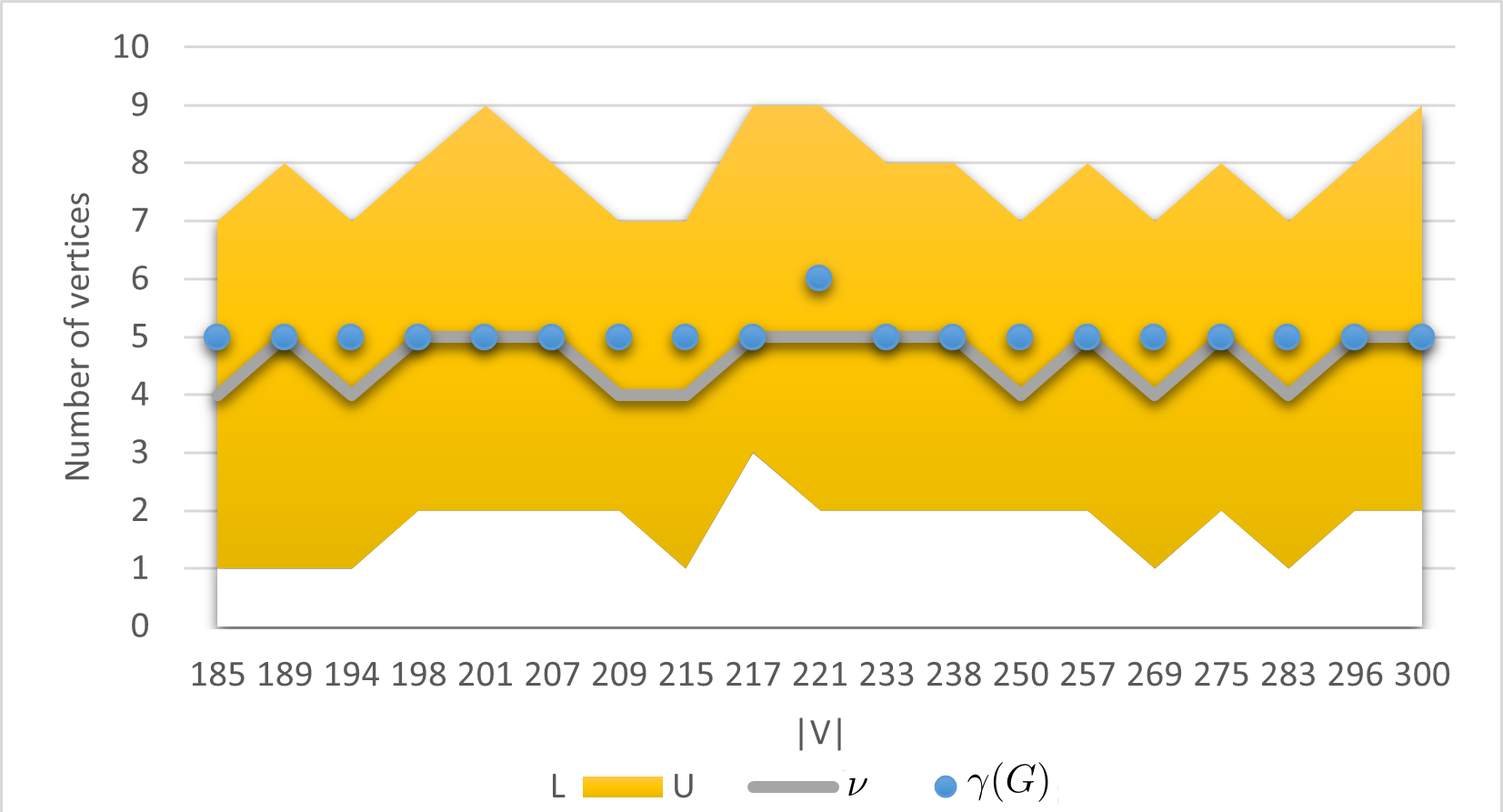
In a simple connected graph $G=(V,E)$, a subset of vertices $S \subseteq V$ is a dominating set if any vertex $v \in V\setminus S$ is adjacent to some vertex $x$ from this subset. A number of real-life problems can be modeled using this problem which is known to be among the difficult NP-hard problems in its class. We formulate the problem as an integer liner program (ILP) and compare the performance with the two earlier existing exact state-of-the-art algorithms and exact implicit enumeration and heuristic algorithms that we propose here. Our exact algorithm was able to find optimal solutions much faster than ILP and the above two exact algorithms for middle-dense instances. For graphs with a considerable size, our heuristic algorithm was much faster than both, ILP and our exact algorithm. It found an optimal solution for more than half of the tested instances, whereas it improved the earlier known state-of-the-art solutions for almost all the tested benchmark instances. Among the instances where the optimum was not found, it gave an average approximation error of $1.18$.
翻译:暂无翻译