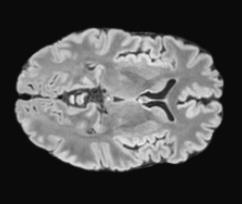
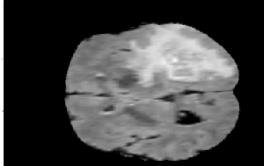
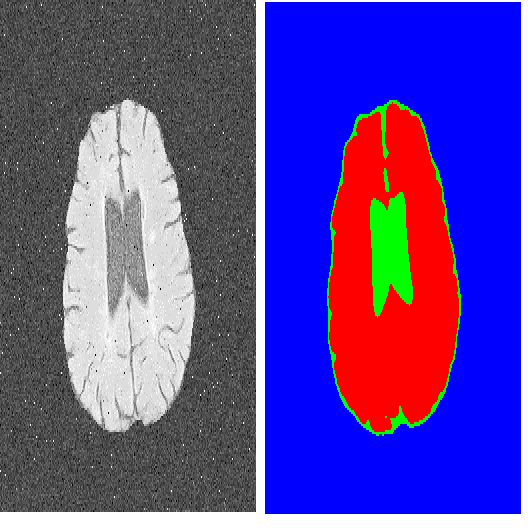
We propose a parameter efficient Bayesian layer for hierarchical convolutional Gaussian Processes that incorporates Gaussian Processes operating in Wasserstein-2 space to reliably propagate uncertainty. This directly replaces convolving Gaussian Processes with a distance-preserving affine operator on distributions. Our experiments on brain tissue-segmentation show that the resulting architecture approaches the performance of well-established deterministic segmentation algorithms (U-Net), which has never been achieved with previous hierarchical Gaussian Processes. Moreover, by applying the same segmentation model to out-of-distribution data (i.e., images with pathology such as brain tumors), we show that our uncertainty estimates result in out-of-distribution detection that outperforms the capabilities of previous Bayesian networks and reconstruction-based approaches that learn normative distributions.
翻译:我们为在瓦塞斯坦-2号空间运行的Gaussian进程提出了一个参数高效贝叶西亚层,该层包含在瓦塞斯坦-2号空间运行的Gaussian进程,以可靠地传播不确定性。这直接取代了Gaussian进程,代之以分布分布上的远程保存松动操作员。我们在脑组织分类方面的实验表明,由此产生的结构结构接近了与先前的高萨进程相比从未实现的成熟的确定分化算法(U-Net ) 的性能。 此外,通过对分配外数据(如脑肿瘤等病理学图像)应用同样的分化模型,我们表明,我们的不确定性估计导致的分流检测超越了先前的巴伊斯网络的能力以及学习规范性分布的重建方法。