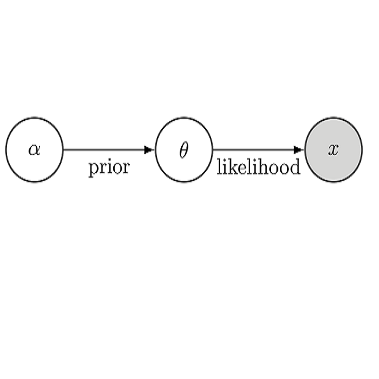
The paper addresses Bayesian inferences in inverse problems with uncertainty quantification involving a computationally expensive forward map associated with solving a partial differential equations. To mitigate the computational cost, the paper proposes a new surrogate model informed by the physics of the problem, specifically when the forward map involves solving a linear elliptic partial differential equation. The study establishes the consistency of the posterior distribution for this surrogate model and demonstrates its effectiveness through numerical examples with synthetic data. The results indicate a substantial improvement in computational speed, reducing the processing time from several months with the exact forward map to a few minutes, while maintaining negligible loss of accuracy in the posterior distribution.
翻译:暂无翻译