Convergent approaches for the Dirichlet Monge ampère problem

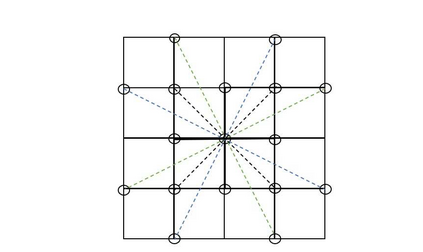
In this article, we introduce and study three numerical methods for the Dirichlet Monge Amp\`ere equation in two dimensions. The approaches consist in considering new equivalent problems. The latter are discretized by a wide stencil finite difference discretization and monotone schemes are obtained. Hence, we apply the Barles-Souganidis theory to prove the convergence of the schemes and the Damped Newtons method is used to compute the solutions of the schemes. Finally, some numerical results are illustrated.