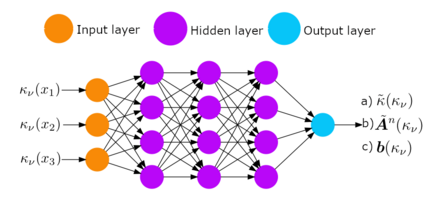
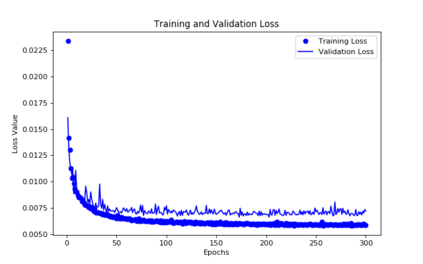
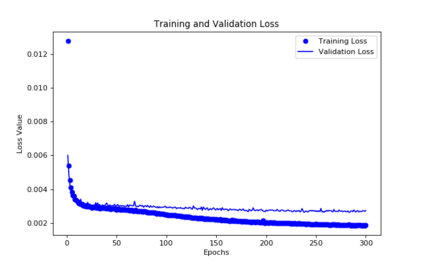
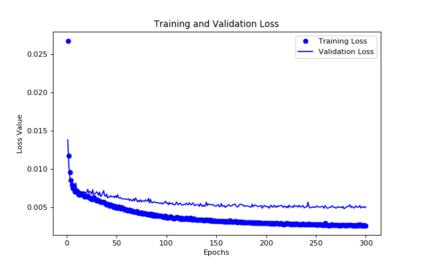
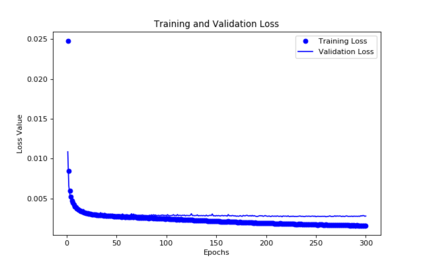
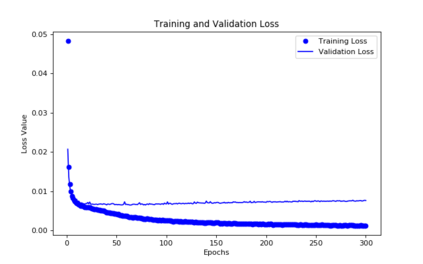
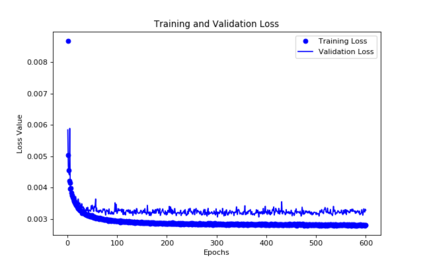
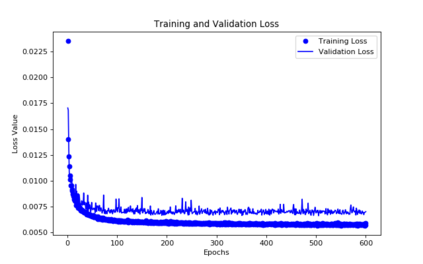
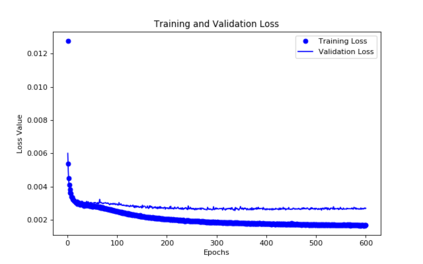
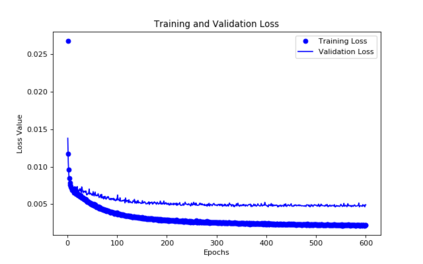
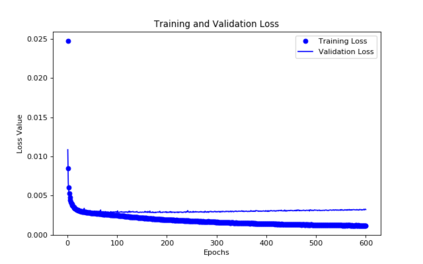
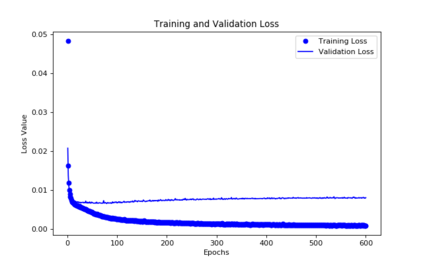
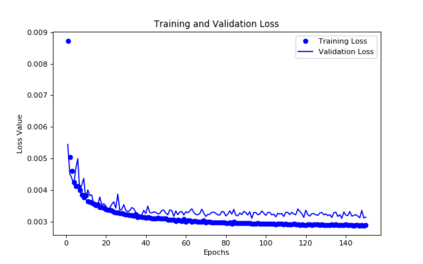
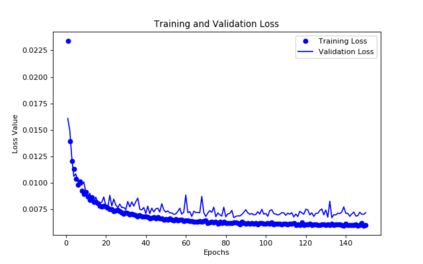
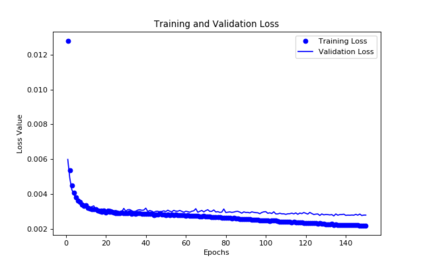
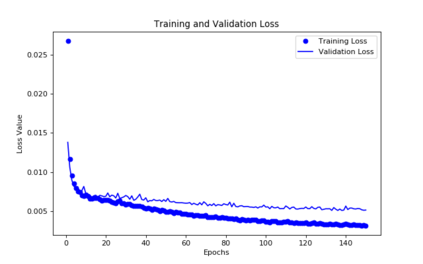
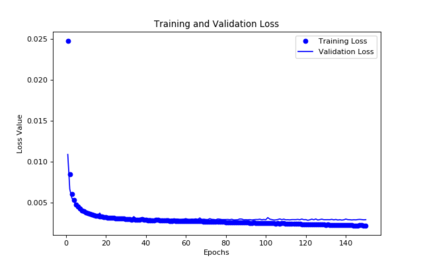
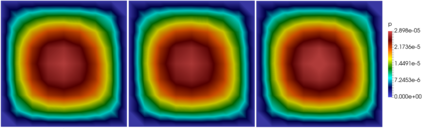
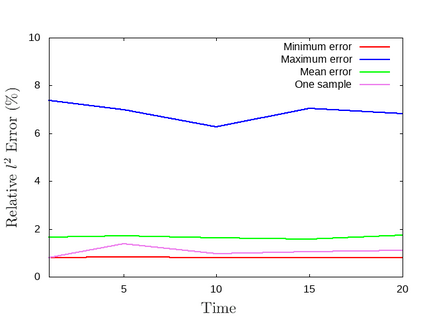
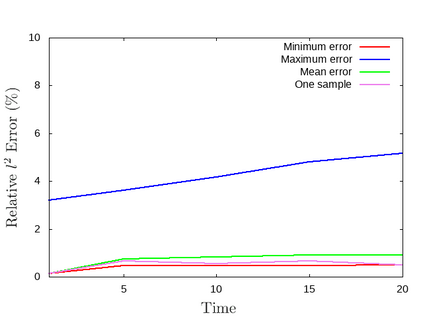
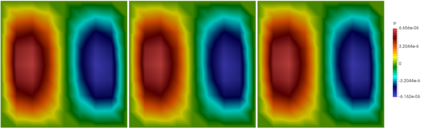
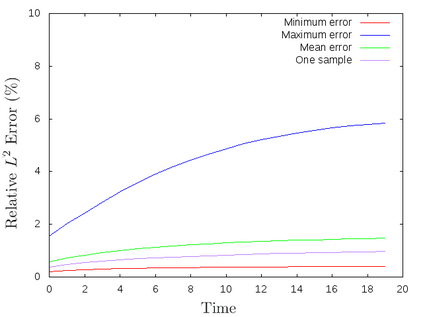
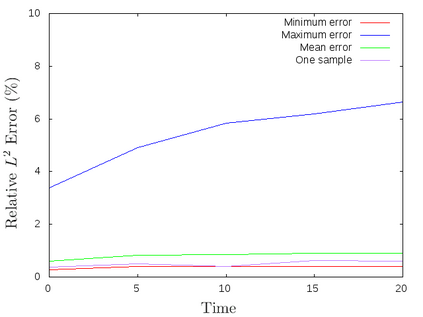
For the nonlinear Richards equation as an unsaturated flow through heterogeneous media, we build a new coarse-scale approximation algorithm utilizing numerical homogenization. This approach follows deep neural networks (DNNs) to quickly and frequently calculate macroscopic parameters. More specifically, we train neural networks with a training set consisting of stochastic permeability realizations and corresponding computed macroscopic targets (effective permeability tensor, homogenized stiffness matrix, and right-hand side vector). Our proposed deep learning scheme develops nonlinear maps between such permeability fields and macroscopic characteristics, and the treatment for Richards equation's nonlinearity is included in the predicted coarse-scale homogenized stiffness matrix, which is a novelty. This strategy's good performance is demonstrated by several numerical tests in two-dimensional model problems, for predictions of the macroscopic properties and consequently solutions.
翻译:对于非线性Richards 等式,作为一个不饱和的通过多种介质流,我们通过数字同质化,建立了一个新的粗尺度近似算法。这个方法遵循深神经网络(DNNs),以快速和经常地计算宏观参数。更具体地说,我们对神经网络进行培训,培训内容包括随机透视性实现和相应的计算宏观目标(有效渗透性强度、同质僵化矩阵和右侧矢量 ) 。我们提议的深层次学习计划开发出在这种渗透性字段和宏观显微特性之间的非线性图,而理查斯等式的非线性治疗则被纳入预测的共性同质僵硬性矩阵中,这是一个新奇特。这一战略的良好表现表现表现表现体现在二维模型问题中的若干数字测试中,用于预测宏观特性和随后的解决方案。