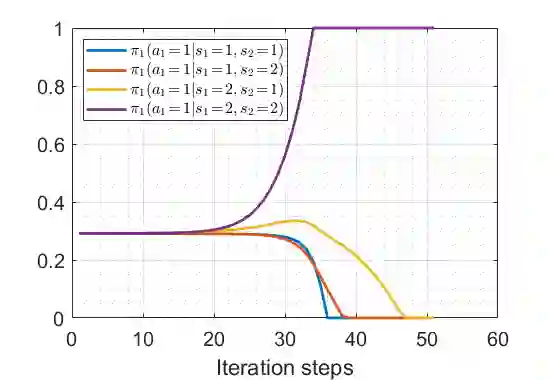
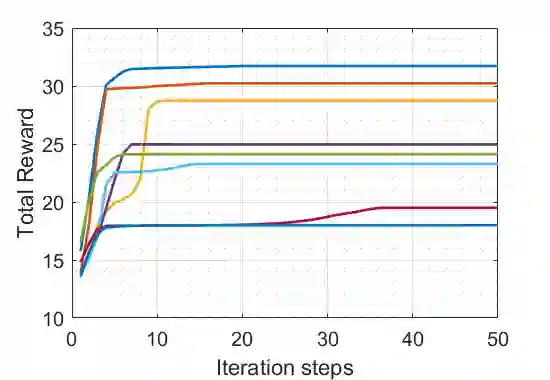
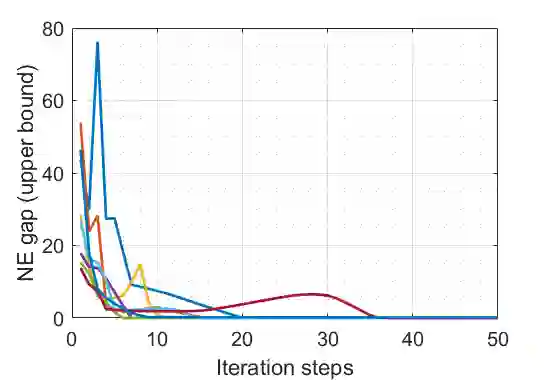
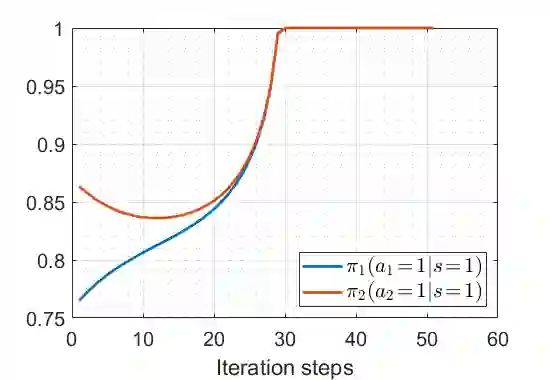
We study the performance of the gradient play algorithm for multi-agent tabular Markov decision processes (MDPs), which are also known as stochastic games (SGs), where each agent tries to maximize its own total discounted reward by making decisions independently based on current state information which is shared between agents. Policies are directly parameterized by the probability of choosing a certain action at a given state. We show that Nash equilibria (NEs) and first order stationary policies are equivalent in this setting, and give a non-asymptotic global convergence rate analysis to an $\epsilon$-NE for a subclass of multi-agent MDPs called Markov potential games, which includes the cooperative setting with identical rewards among agents as an important special case. Our result shows that the number of iterations to reach an $\epsilon$-NE scales linearly, instead of exponentially, with the number of agents. Local geometry and local stability are also considered. For Markov potential games, we prove that strict NEs are local maxima of the total potential function and fully-mixed NEs are saddle points. We also give a local convergence rate around strict NEs for more general settings.
翻译:我们研究多试剂表单马可夫决策程序(MDPs)的梯度游戏算法的性能,该算法也称为随机游戏(SGs),每个代理商都试图通过独立地根据代理商之间共享的当前状态信息做出决策,最大限度地提高自己的全部折扣奖励。政策直接以在某个特定国家选择某种行动的概率为参数。我们显示Nash equilibria(NES)和一阶固定政策在这个环境中是等效的,并且对一个称为Markov 潜在MDPs子类的分级分级分级的分级分级的分级分级公司($/epsilon-NE)进行非零星($-NE)趋同率分析,该分级游戏称为Markov 潜在MDPs,其中包括在代理商之间以相同奖励的合作设置,作为一个重要的特殊案例。我们的结果显示,线度达到美元-NEE的升标数,而不是指数,与代理商数是相等的。当地测地测量和当地稳定政策也考虑。关于Markov潜在游戏,我们证明严格的NE是总潜在功能和完全混合NEEEV是固定的局部标准。