On Accelerating Distributed Convex Optimizations

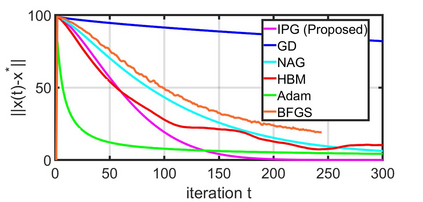
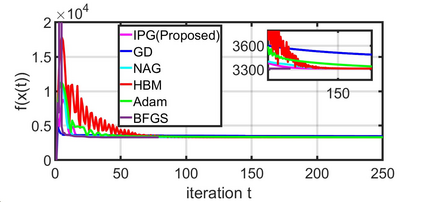
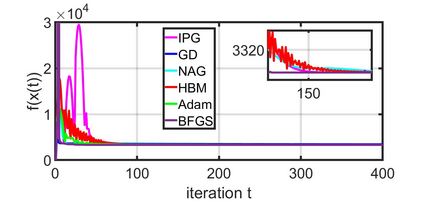
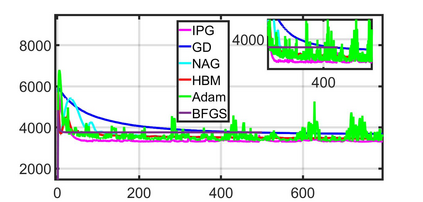
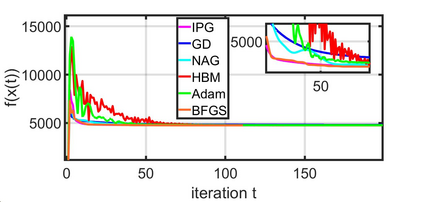
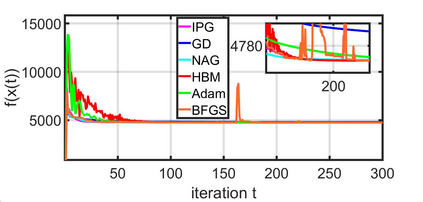
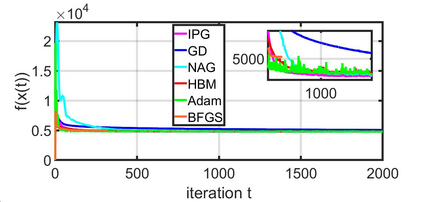
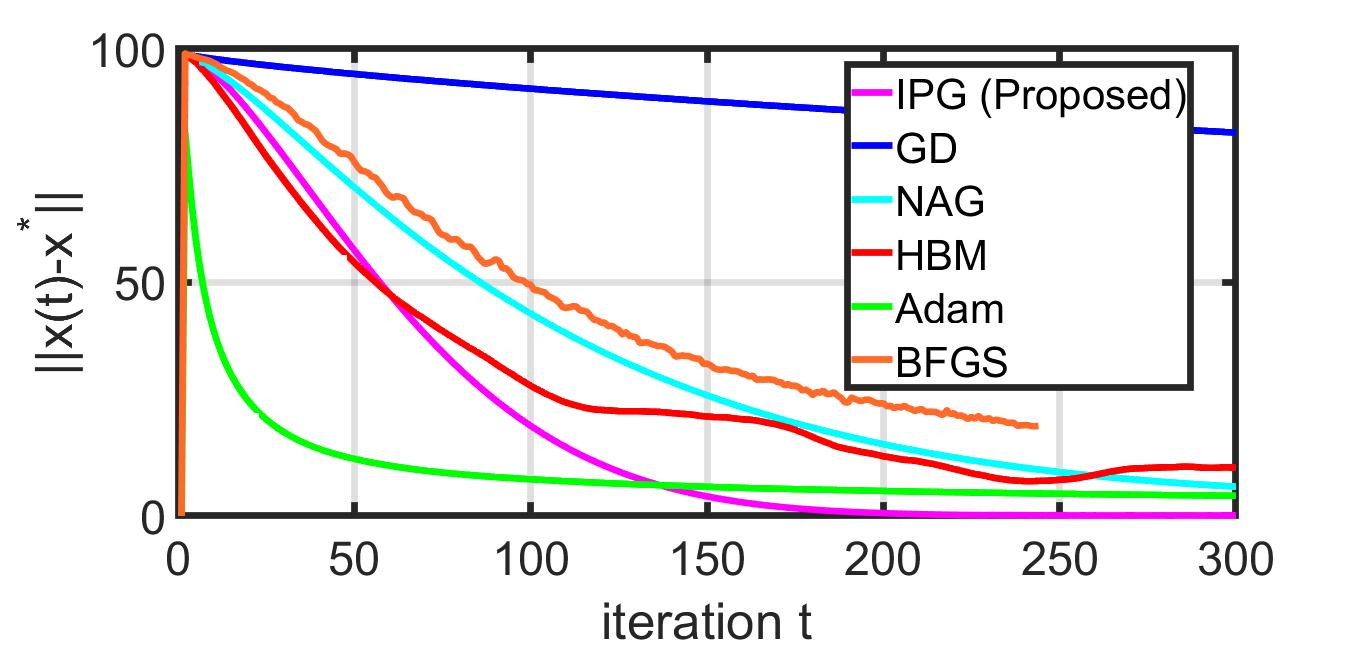
This paper studies a distributed multi-agent convex optimization problem. The system comprises multiple agents in this problem, each with a set of local data points and an associated local cost function. The agents are connected to a server, and there is no inter-agent communication. The agents' goal is to learn a parameter vector that optimizes the aggregate of their local costs without revealing their local data points. In principle, the agents can solve this problem by collaborating with the server using the traditional distributed gradient-descent method. However, when the aggregate cost is ill-conditioned, the gradient-descent method (i) requires a large number of iterations to converge, and (ii) is highly unstable against process noise. We propose an iterative pre-conditioning technique to mitigate the deleterious effects of the cost function's conditioning on the convergence rate of distributed gradient-descent. Unlike the conventional pre-conditioning techniques, the pre-conditioner matrix in our proposed technique updates iteratively to facilitate implementation on the distributed network. In the distributed setting, we provably show that the proposed algorithm converges linearly with an improved rate of convergence than the traditional and adaptive gradient-descent methods. Additionally, for the special case when the minimizer of the aggregate cost is unique, our algorithm converges superlinearly. We demonstrate our algorithm's superior performance compared to prominent distributed algorithms for solving real logistic regression problems and emulating neural network training via a noisy quadratic model, thereby signifying the proposed algorithm's efficiency for distributively solving non-convex optimization. Moreover, we empirically show that the proposed algorithm results in faster training without compromising the generalization performance.