Contextual Dynamic Pricing: Algorithms, Optimality, and Local Differential Privacy Constraints

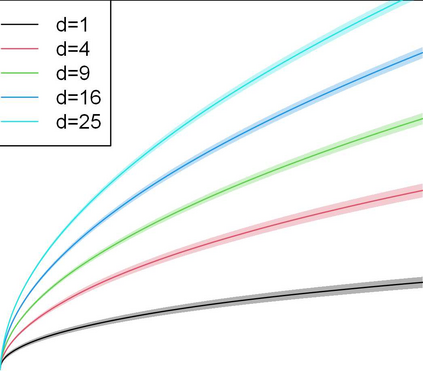
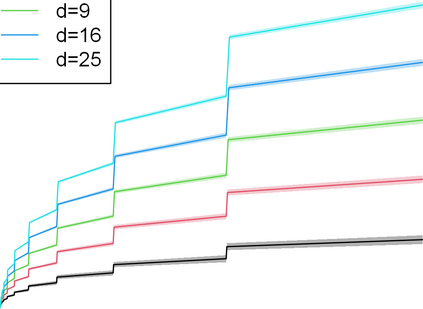
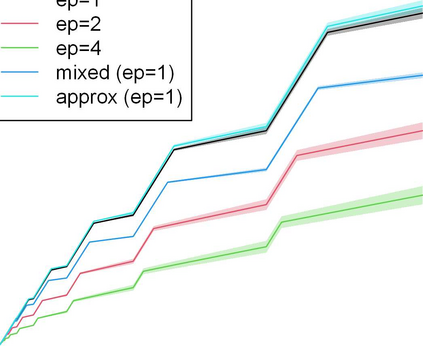
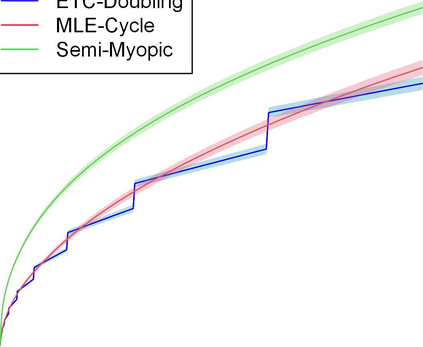
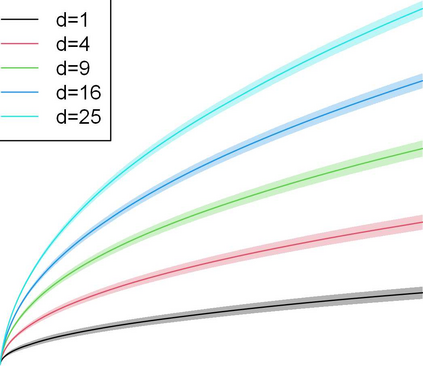
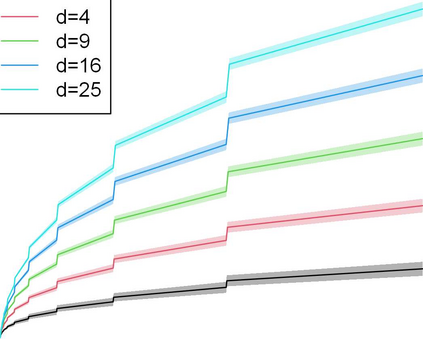
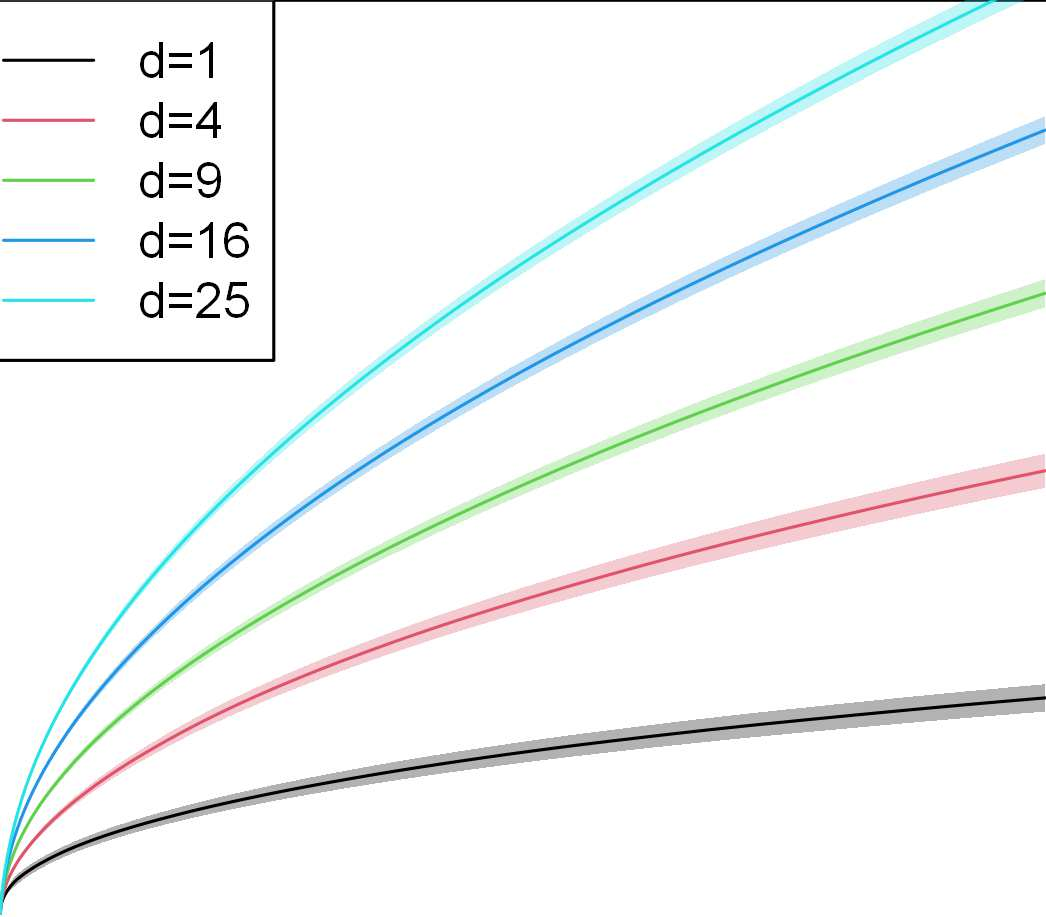
We study contextual dynamic pricing problems where a firm sells products to $T$ sequentially-arriving consumers, behaving according to an unknown demand model. The firm aims to minimize its regret over a clairvoyant that knows the model in advance. The demand follows a generalized linear model (GLM), allowing for stochastic feature vectors in $\mathbb R^d$ encoding product and consumer information. We first show the optimal regret is of order $\sqrt{dT}$, up to logarithmic factors, improving existing upper bounds by a $\sqrt{d}$ factor. This optimal rate is materialized by two algorithms: a confidence bound-type algorithm and an explore-then-commit (ETC) algorithm. A key insight is an intrinsic connection between dynamic pricing and contextual multi-armed bandit problems with many arms with a careful discretization. We further study contextual dynamic pricing under local differential privacy (LDP) constraints. We propose a stochastic gradient descent-based ETC algorithm achieving regret upper bounds of order $d\sqrt{T}/\epsilon$, up to logarithmic factors, where $\epsilon>0$ is the privacy parameter. The upper bounds with and without LDP constraints are matched by newly constructed minimax lower bounds, characterizing costs of privacy. Moreover, we extend our study to dynamic pricing under mixed privacy constraints, improving the privacy-utility tradeoff by leveraging public data. This is the first time such setting is studied in the dynamic pricing literature and our theoretical results seamlessly bridge dynamic pricing with and without LDP. Extensive numerical experiments and real data applications are conducted to illustrate the efficiency and practical value of our algorithms.