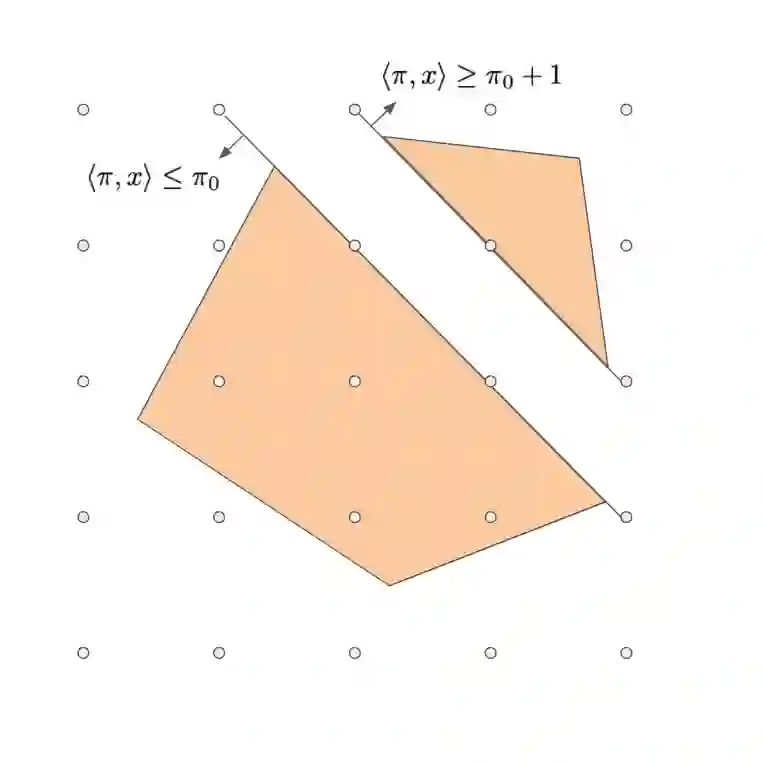
A \emph{general branch-and-bound tree} is a branch-and-bound tree which is allowed to use general disjunctions of the form $\pi^{\top} x \leq \pi_0 \,\vee\, \pi^{\top}x \geq \pi_0 + 1$, where $\pi$ is an integer vector and $\pi_0$ is an integer scalar, to create child nodes. We construct a packing instance, a set covering instance, and a Traveling Salesman Problem instance, such that any general branch-and-bound tree that solves these instances must be of exponential size. We also verify that an exponential lower bound on the size of general branch-and-bound trees persists when we add Gaussian noise to the coefficients of the cross polytope, thus showing that polynomial-size "smoothed analysis" upper bound is not possible. The results in this paper can be viewed as the branch-and-bound analog of the seminal paper by Chv\'atal et al. \cite{chvatal1989cutting}, who proved lower bounds for the Chv\'atal-Gomory rank.
翻译:\ emph{ 普通分支和绑定树} 是一个分支和捆绑树, 它允许使用 $\ pi ⁇ top} x\leq\ pi_ 0\\\\\ vee\,\\ pi ⁇ to} x\geq\ pi_ 0+ 1$, $\ pi_ 0 + 1$ 是整数矢量, $\ pi_ 0 是一个整数斜度, 以创建子节点。 我们构建了一个包装实例, 一套覆盖实例, 和一个旅行销售员问题实例, 任何解决这些情形的普通分支和绑定树必须具有指数大小 。 我们还核查当我们将高斯噪音加到跨多彩形的系数中时, 当我们把高尔西亚的噪音加到圆形的系数中时, $\ pi_ pi_ 0$ 是不可能创建子节点节点。 本文的结果可以被视为 Chvry\ at 和 cal- gal- greal- cal- greal- gretraction 证明Cal- hol- goal- pal- gas- gal- gal- pal- pal- pal- gourt- gourt- gourt- gourt_____c_ grout)