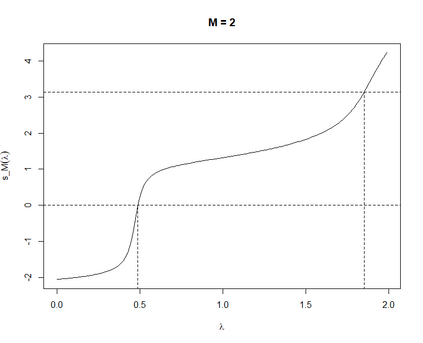
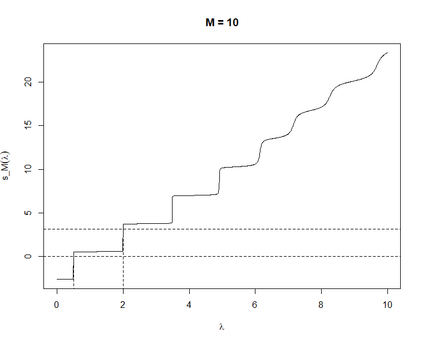
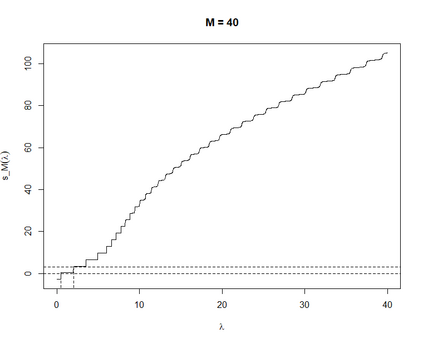
We investigate the stability of quasi-stationary distributions of killed Markov processes to perturbations of the generator. In the first setting, we consider a general bounded self-adjoint perturbation operator, and after that, study a particular unbounded perturbation corresponding to the truncation of the killing rate. In both scenarios, we quantify the difference between eigenfunctions of the smallest eigenvalue of the perturbed and unperturbed generator in a Hilbert space norm. As a consequence, $\mathcal{L}^1$-norm estimates of the difference of the resulting quasi-stationary distributions in terms of the perturbation are provided. These results are particularly relevant to the recently-proposed class of quasi-stationary Monte Carlo methods, designed for scalable exact Bayesian inference.
翻译:我们调查了被杀死的Markov过程的半静止分布的稳定性,以干扰发电机。 在第一个设置中,我们考虑的是一般封闭的自我联合扰动操作员,然后研究一个与杀人率脱节相对应的未受约束的扰动器。在这两种情况下,我们量化了在Hilbert空间规范中受扰动和无扰动发电机最小的基因值之间的差别。因此,我们提供了对由此造成的半静止分布在扰动率方面的差异的美元=mathcal{L ⁇ 1$-norm估计值。这些结果与最近拟订的半静止蒙特卡洛方法类别特别相关,该类方法的设计是为了进行可变缩缩的贝叶斯的精确推断。