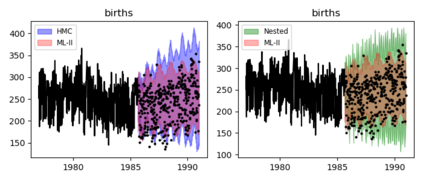
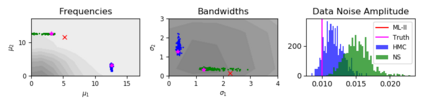
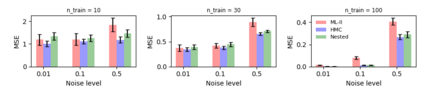
Gaussian Process (GPs) models are a rich distribution over functions with inductive biases controlled by a kernel function. Learning occurs through the optimisation of kernel hyperparameters using the marginal likelihood as the objective. This classical approach known as Type-II maximum likelihood (ML-II) yields point estimates of the hyperparameters, and continues to be the default method for training GPs. However, this approach risks underestimating predictive uncertainty and is prone to overfitting especially when there are many hyperparameters. Furthermore, gradient based optimisation makes ML-II point estimates highly susceptible to the presence of local minima. This work presents an alternative learning procedure where the hyperparameters of the kernel function are marginalised using Nested Sampling (NS), a technique that is well suited to sample from complex, multi-modal distributions. We focus on regression tasks with the spectral mixture (SM) class of kernels and find that a principled approach to quantifying model uncertainty leads to substantial gains in predictive performance across a range of synthetic and benchmark data sets. In this context, nested sampling is also found to offer a speed advantage over Hamiltonian Monte Carlo (HMC), widely considered to be the gold-standard in MCMC based inference.
翻译:Gausian Process (GPs) 模型在功能上分布丰富,带有内核功能控制的感应偏差。 学习是通过优化内核超分计, 使用边际可能性作为目标。 这种古典方法被称为二型最大可能性(ML-II) 生成超分数估计, 继续是培训GP的默认方法。 但是, 这种方法有可能低估预测不确定性, 并且容易过度适应, 特别是在有许多超光谱参数的情况下。 此外, 基于梯度的优化使 ML- II 点估计极易受到本地微型数据的存在。 这项工作提出了一种替代性学习程序, 将内核功能的超单数利用Nested抽样(NS) 进行边缘化, 这是一种非常适合复杂、 多式分布样本的技术。 我们注重光谱混合物类的回归任务, 并发现对模型不确定性进行量化的原则性方法, 导致在一系列合成和基准数据集的预测性性工作上取得重大收益。 在这种背景下, 以 IMFMARM 标准 模型 的取样还被认为具有超越了 标准 。