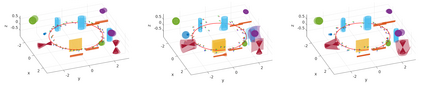
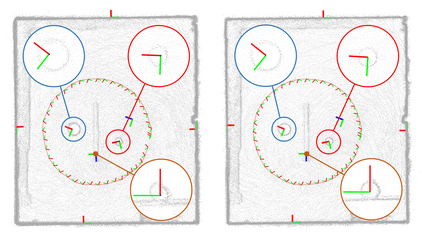
In Simultaneous Localization And Mapping (SLAM) problems, high-level landmarks have the potential to build compact and informative maps compared to traditional point-based landmarks. In this work, we focus on the parameterization of frequently used geometric primitives including points, lines, planes, ellipsoids, cylinders, and cones. We first present a unified representation based on quadrics, leading to a consistent and concise formulation. Then we further study a decomposed model of quadrics that discloses the symmetric and degenerated properties of a primitive. Based on the decomposition, we develop geometrically meaningful quadrics factors in the settings of a graph-SLAM problem. Then in simulation experiments, it is shown that the decomposed formulation has better efficiency and robustness to observation noises than baseline parameterizations. Finally, in real-world experiments, the proposed back-end framework is demonstrated to be capable of building compact and regularized maps.
翻译:在同步本地化和绘图(SLAM)问题中,高层次的地标与传统的点基地标相比,有可能绘制紧凑而翔实的地图。在这项工作中,我们侧重于经常使用的几何原始点的参数化,包括点、线条、平面、椭球、圆柱和锥形。我们首先根据四分法提出一个统一的表示法,导致一个一致和简洁的配方。然后我们进一步研究一个分解的四分法模型,揭示一个原始的对称和退化特性。根据分解法,我们在图形-SLAM问题的环境中开发了具有几何意义的四分法因素。然后在模拟实验中显示,分解的配方比基线参数化更具有效率和稳健性。最后,在现实世界的实验中,拟议的后端框架证明能够建立紧凑和正规的地图。