New Tools for Smoothed Analysis: Least Singular Value Bounds for Random Matrices with Dependent Entries

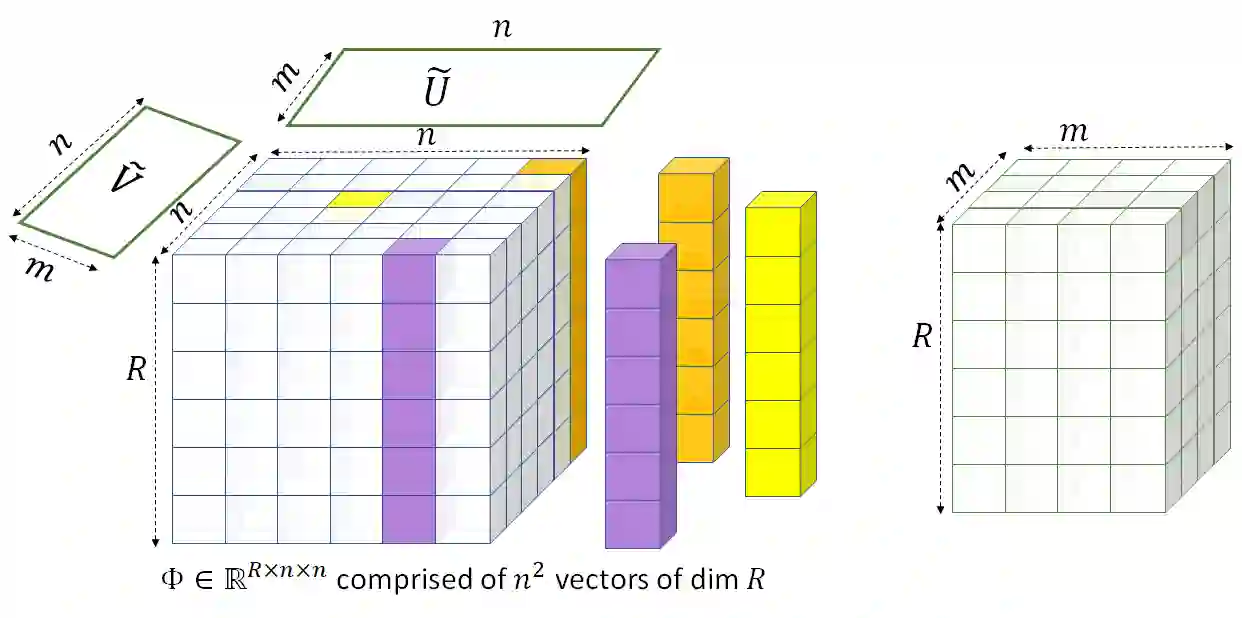
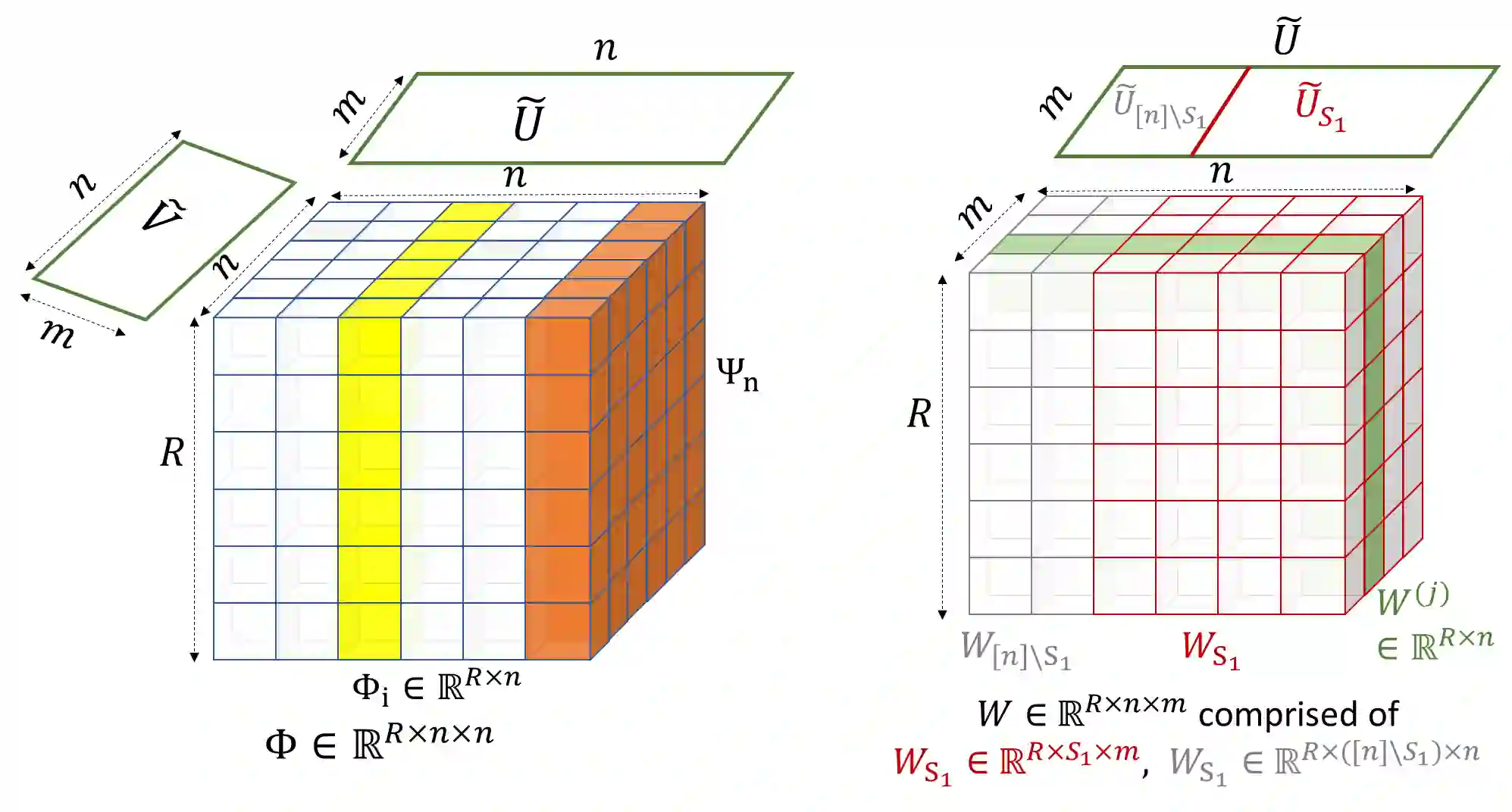
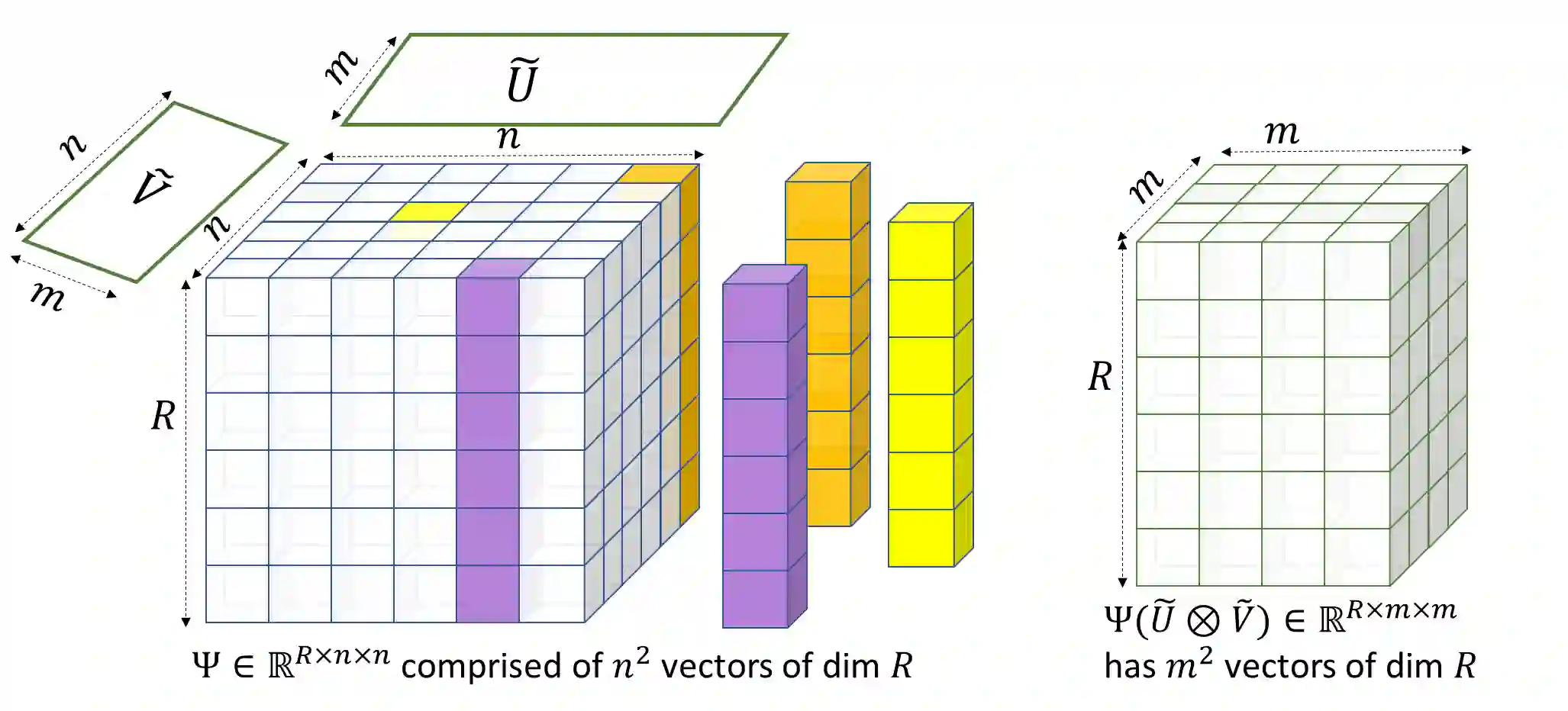
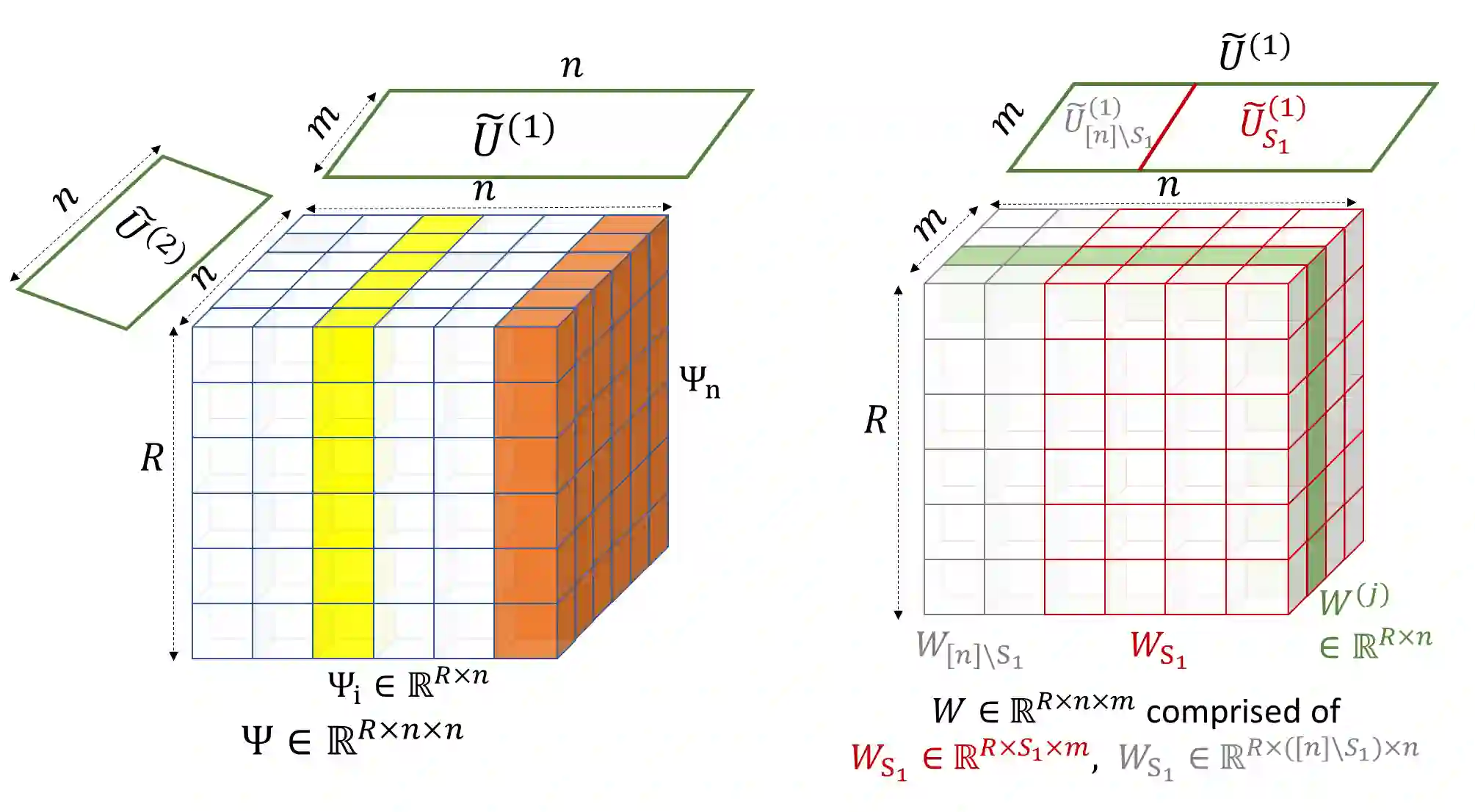
We develop new techniques for proving lower bounds on the least singular value of random matrices with limited randomness. The matrices we consider have entries that are given by polynomials of a few underlying base random variables. This setting captures a core technical challenge for obtaining smoothed analysis guarantees in many algorithmic settings. Least singular value bounds often involve showing strong anti-concentration inequalities that are intricate and much less understood compared to concentration (or large deviation) bounds. First, we introduce a general technique involving a hierarchical $\epsilon$-nets to prove least singular value bounds. Our second tool is a new statement about least singular values to reason about higher-order lifts of smoothed matrices, and the action of linear operators on them. Apart from getting simpler proofs of existing smoothed analysis results, we use these tools to now handle more general families of random matrices. This allows us to produce smoothed analysis guarantees in several previously open settings. These include new smoothed analysis guarantees for power sum decompositions, subspace clustering and certifying robust entanglement of subspaces, where prior work could only establish least singular value bounds for fully random instances or only show non-robust genericity guarantees.