Reduced-bias estimation of the residual dependence index with unnamed marginals

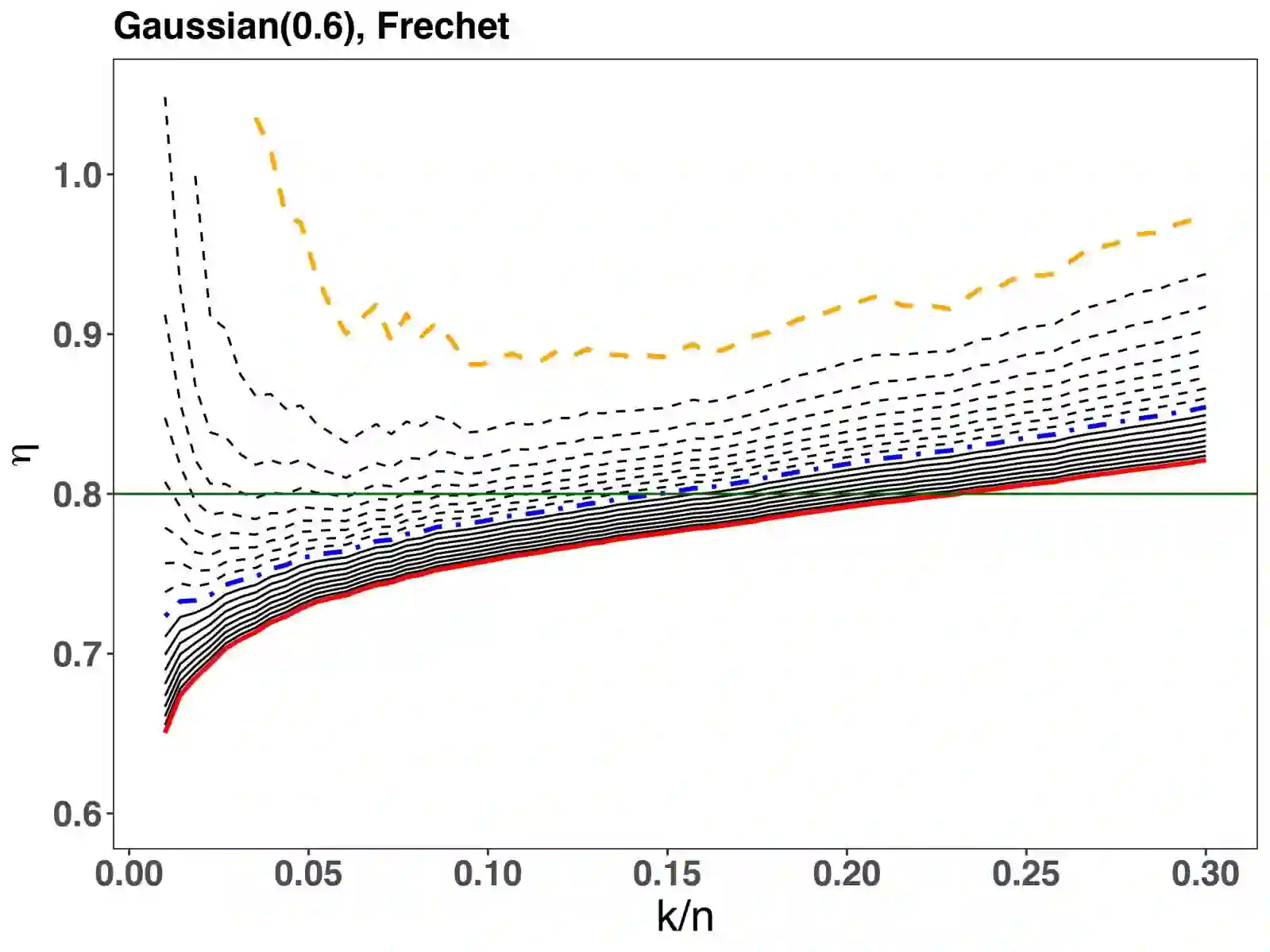
This paper addresses important weaknesses in current methodology for the estimation of multivariate extreme event distributions. The estimation of the residual dependence index $\eta \in (0,1]$ is notoriously problematic. We introduce a flexible class of reduced-bias estimators for this parameter, designed to ameliorate the usual problems of threshold selection through a unified approach to the familiar margins standardisation. We derive the associated asymptotic properties. The efficacy of the proposed semi-parametric inference on $\eta$ stems from a hitherto neglected exponentially decaying term in the hidden regular variation characterisation. Simulation studies to assess the performance for finite samples over a range of standard copulas indicate an improved performance, relative to the existing standard methods such as the Hill estimator. Our leading application illustrates how asymptotic independence can be discerned from monsoon-related rainfall occurrences at different locations in Ghana. The considerations involved in extending this framework to feasible inference on the extreme value index attached to domains of attraction are briefly discussed.