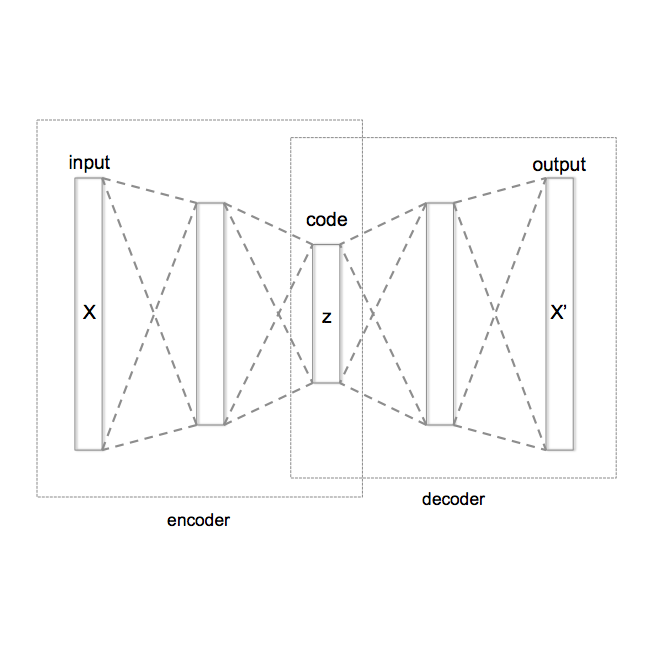
Geometric transformations have been widely used to augment the size of training images. Existing methods often assume a unimodal distribution of the underlying transformations between images, which limits their power when data with multimodal distributions occur. In this paper, we propose a novel model, Multimodal Geometric Augmentation (MGAug), that for the first time generates augmenting transformations in a multimodal latent space of geometric deformations. To achieve this, we first develop a deep network that embeds the learning of latent geometric spaces of diffeomorphic transformations (a.k.a. diffeomorphisms) in a variational autoencoder (VAE). A mixture of multivariate Gaussians is formulated in the tangent space of diffeomorphisms and serves as a prior to approximate the hidden distribution of image transformations. We then augment the original training dataset by deforming images using randomly sampled transformations from the learned multimodal latent space of VAE. To validate the efficiency of our model, we jointly learn the augmentation strategy with two distinct domain-specific tasks: multi-class classification on 2D synthetic datasets and segmentation on real 3D brain magnetic resonance images (MRIs). We also compare MGAug with state-of-the-art transformation-based image augmentation algorithms. Experimental results show that our proposed approach outperforms all baselines by significantly improved prediction accuracy. Our code is publicly available at https://github.com/tonmoy-hossain/MGAug.
翻译:暂无翻译