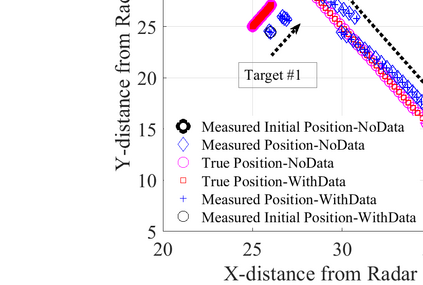
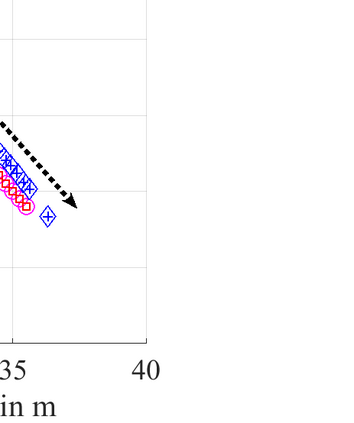
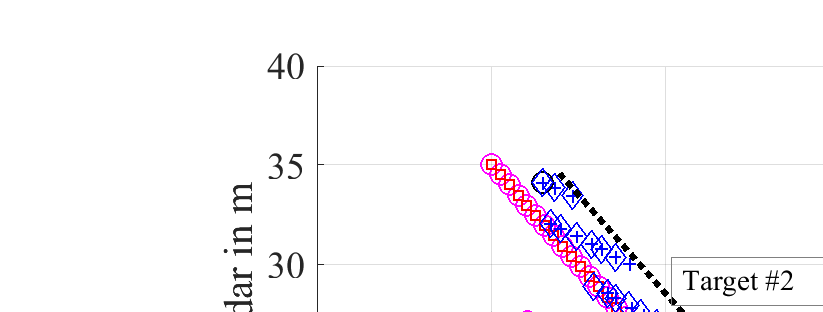
In this paper, we derive the information theoretic performance bounds on communication data rates and errors in parameter estimation, for a joint radar and communication (JRC) system. We assume that targets are semi-passive, i.e. they use active components for signal reception, and passive components to communicate their own information. Specifically, we let the targets to have control over their passive reflectors in order to transmit their own information back to the radar via reflection-based beamforming or backscattering. We derive the Cramer-Rao lower bounds (CRBs) for the mean squared error in the estimation of target parameters. The concept of a target ambiguity function (TAF) arises naturally in the derivation CRBs. Using these TAFs as cost function, we propose a waveform optimization technique based on calculus of variations. Further, we derive lower bounds on the data rates for communication on forward and reverse channels, in radar-only and joint radar and communications scenarios. Through numerical examples, we demonstrate the utility of this framework for transmit waveform design, codebook construction, and establishing the corresponding data rate bounds.
翻译:在本文中,我们从通信数据率和参数估计差错中得出关于联合雷达和通信系统(JRC)的通信数据率和参数估计差错的信息理论性能界限;我们假定目标为半被动性,即它们使用主动的信号接收元件和被动的元件来传送自己的信息;具体地说,我们让目标对其被动反射器进行控制,以便通过反射波成形或反射将自己的信息反馈雷达;我们从目标参数估计平均平方错误中得出Cramer-RABs(CRBs)下限。目标模糊功能的概念自然产生于衍生的CRBs。我们利用这些TAF作为成本函数,提出一种以变异微分为基础的波形优化技术。此外,我们在雷达和联合雷达及通信假设中,对前向和反向频道的通信数据率的下限。我们通过数字示例展示了这一框架在传输波形设计、代码表构建和确定相应数据率约束方面的实用性。