Parameterizing and Simulating from Causal Models

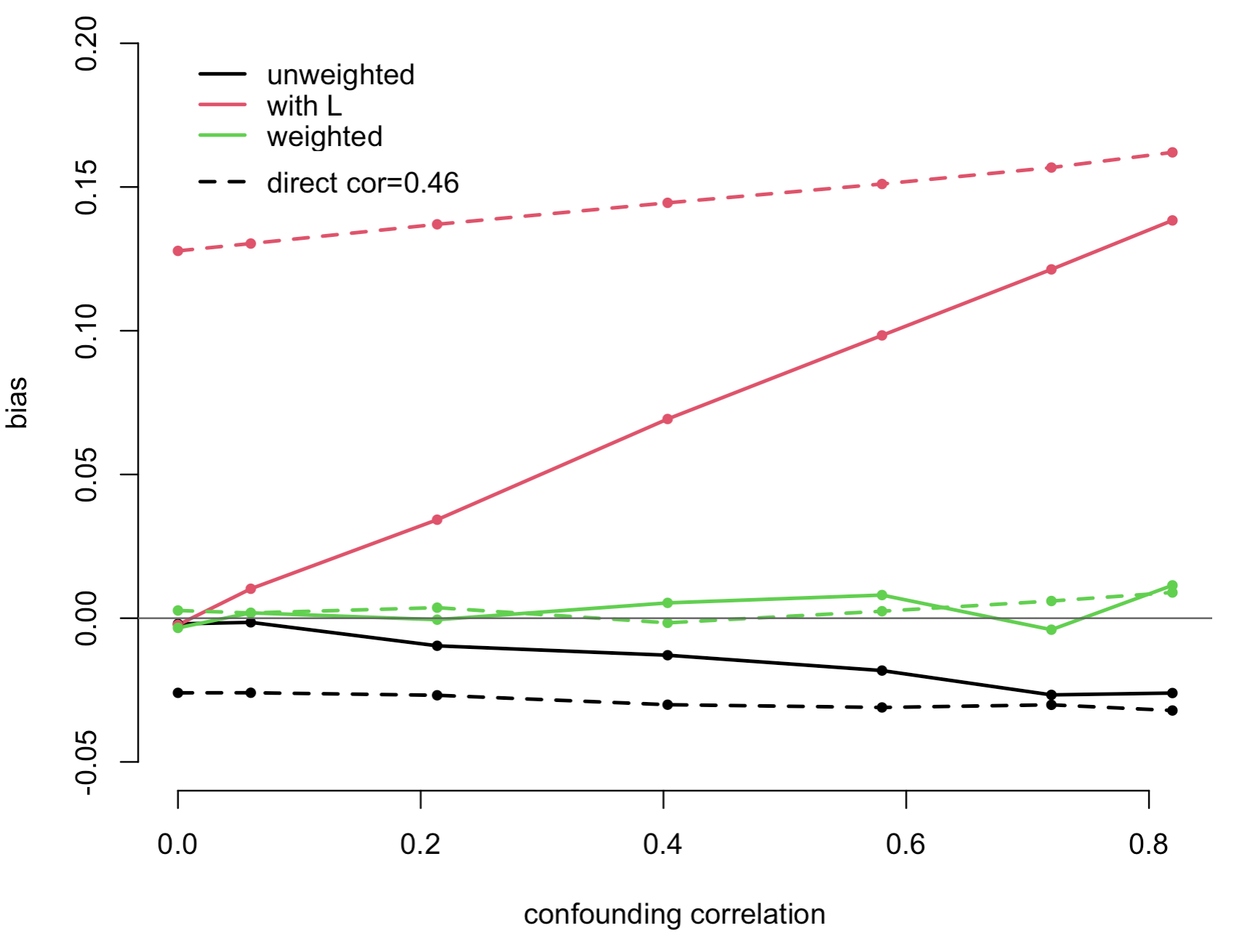
Many statistical problems in causal inference involve a probability distribution other than the one from which data are actually observed; as an additional complication, the object of interest is often a marginal quantity of this other probability distribution. This creates many practical complications for statistical inference, even where the problem is non-parametrically identified. Na\"ive attempts to specify a model parametrically can lead to unwanted consequences such as incompatible parametric assumptions or the so-called `g-null paradox'. As a consequence it is difficult to perform likelihood-based inference, or even to simulate from the model in a general way. We introduce the `frugal parameterization', which places the causal effect of interest at its centre, and then build the rest of the model around it. We do this in a way that provides a recipe for constructing a regular, non-redundant parameterization using causal quantities of interest. In the case of discrete variables we use odds ratios to complete the parameterization, while in the continuous case we use copulas. Our methods allow us to construct and simulate from models with parametrically specified causal distributions, and fit them using likelihood-based methods, including fully Bayesian approaches. Models we can fit and simulate from exactly include marginal structural models and structural nested models. Our proposal includes parameterizations for the average causal effect and effect of treatment on the treated, as well as other causal quantities of interest. Our results will allow practitioners to assess their methods against the best possible estimators for correctly specified models, in a way which has previously been impossible.