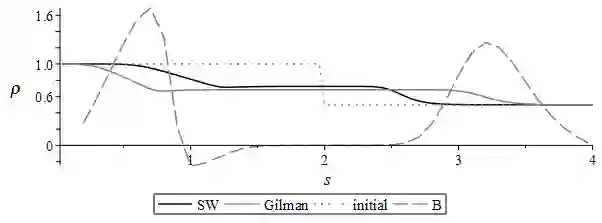
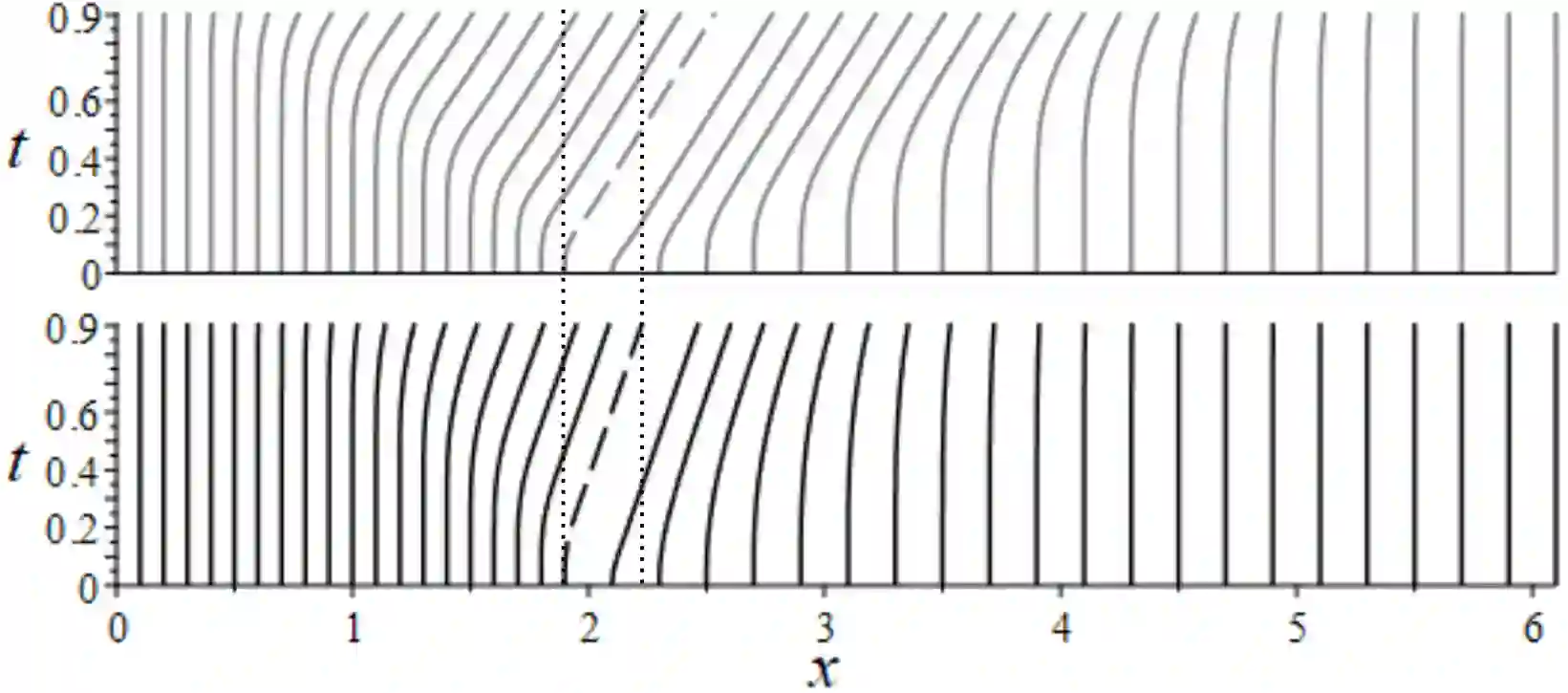
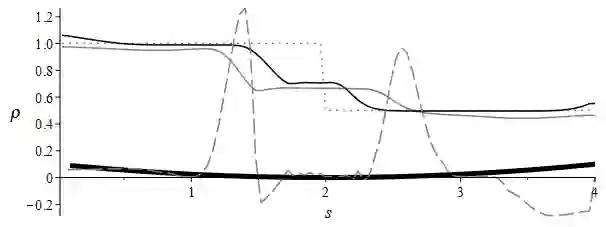
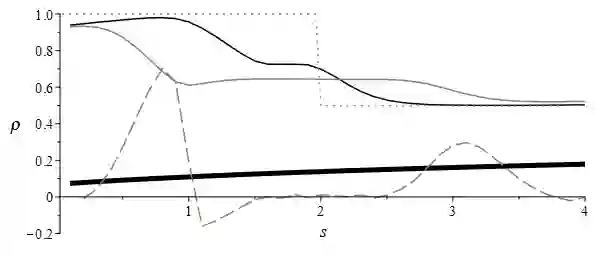
Invariant finite-difference schemes for the one-dimensional shallow water equations in the presence of a magnetic field for various bottom topographies are constructed. Based on the results of the group classification recently carried out by the authors, finite-difference analogues of the conservation laws of the original differential model are obtained. Some typical problems are considered numerically, for which a comparison is made between the cases of a magnetic field presence and when it is absent (the standard shallow water model). The invariance of difference schemes in Lagrangian coordinates and the energy preservation on the obtained numerical solutions are also discussed.
翻译:本文考虑一维狭浅水方程在磁场作用下在不同海底地形条件下的有限差分方案。在对称群分类的基础上,本文得到其守恒律的有限差分形式,所得差分方案具有拉格朗日坐标下的不变性和能量守恒性质。本文将差分方案应用于实际问题中,比较了磁场和非磁场问题的数值解,讨论了能量在数值解上的保存情况。