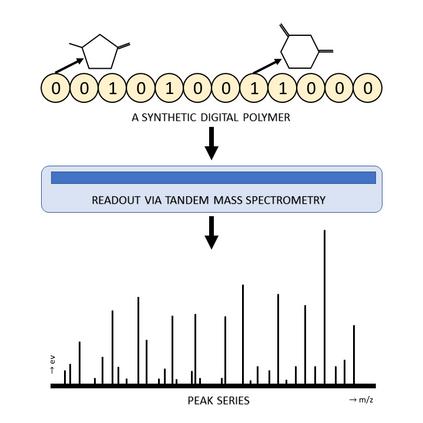
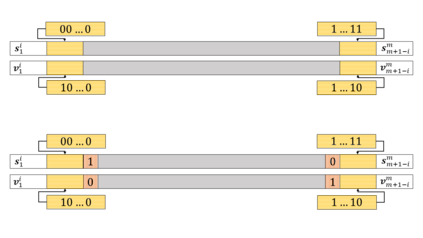
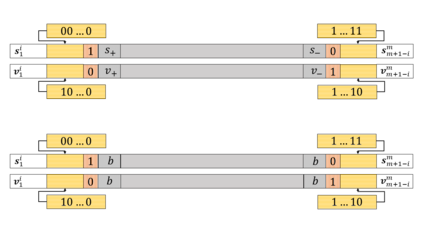
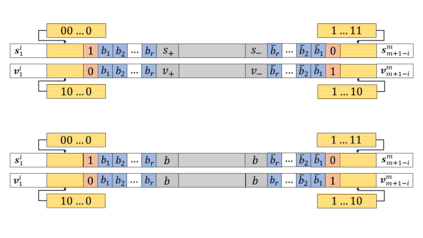
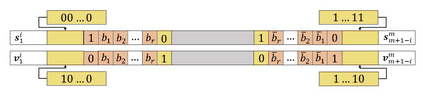
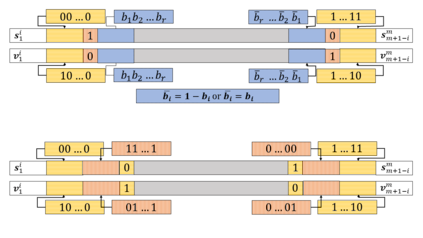
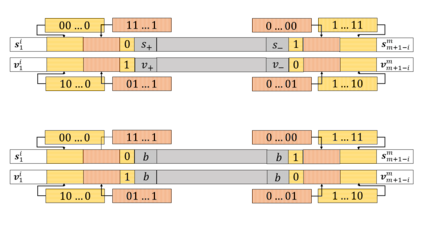
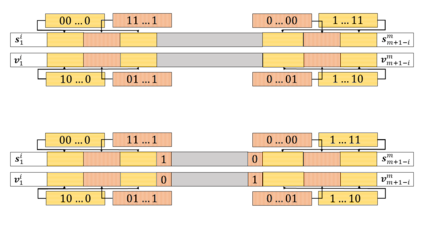
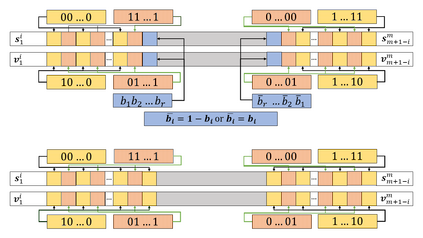
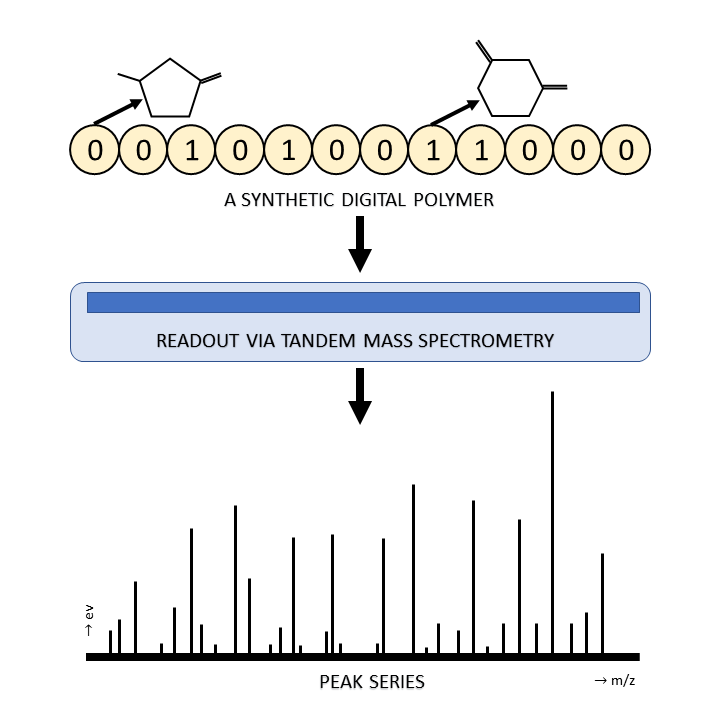
Motivated by polymer-based data-storage platforms that use chains of binary synthetic polymers as the recording media and read the content via tandem mass spectrometers, we propose a new family of codes that allows for both unique string reconstruction and correction of multiple mass errors. We consider two approaches: The first approach pertains to asymmetric errors and it is based on introducing redundancy that scales linearly with the number of errors and logarithmically with the length of the string. The construction allows for the string to be uniquely reconstructed based only on its erroneous substring composition multiset. The key idea behind our unique reconstruction approach is to interleave (shifted) Catalan-Bertrand paths with arbitrary binary strings and "reflect" them so as to force prefixes and suffixes of the same length to have different weights. The asymptotic code rate of the scheme is one, and decoding is accomplished via a simplified version of the backtracking algorithm used for the Turnpike problem. For symmetric errors, we use a polynomial characterization of the mass information and adapt polynomial evaluation code constructions for this setting. In the process, we develop new efficient decoding algorithms for a constant number of composition errors and show that the redundancy of the scheme scales quadratically with the number of errors and logarithmically with the codelength.
翻译:基于聚合物的数据存储平台将二进制合成聚合物链用作记录介质,通过同步质谱仪阅读内容,我们为此提出一套新的代码,既允许独特的字符串重建,又允许纠正多个质量错误。我们考虑两种方法:第一种方法涉及不对称错误,其依据是引入冗余,以线性尺度与错误数量和对数与字符串长度相匹配。这一构建允许仅根据其错误的子字符串组成多重设置,对字符串进行独特的重建。我们独特的重建方法的关键思想是使用任意的双弦字符串和“反射”的中间线(变换)加泰罗兰-伯特路径,以便强制进行前缀和相同长度的后缀,使其具有不同的重量。这个方法的无序编码率与错误数量相匹配,通过简化的回溯算算算算算法来完成解码。对于测错,我们使用一个多式的卡通-白路径来描述质量信息,并调整一个连续的算法模型的公式,用于我们制定一个持续解算法结构的公式,用于构建一个不断的定序的公式,用于我们定序的定序的定序的平比值的公式。