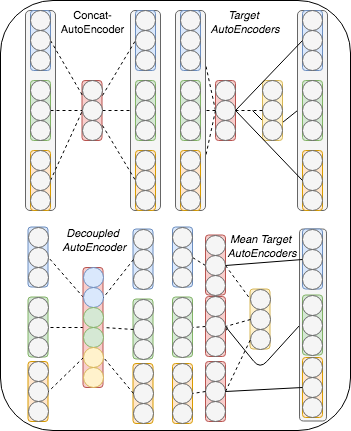
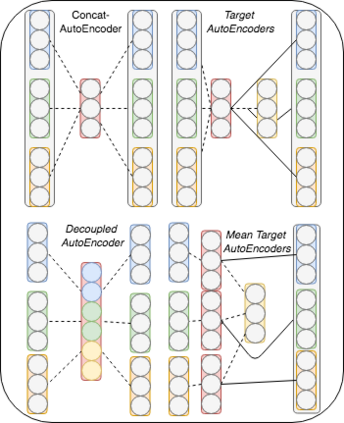
Ensembling word embeddings to improve distributed word representations has shown good success for natural language processing tasks in recent years. These approaches either carry out straightforward mathematical operations over a set of vectors or use unsupervised learning to find a lower-dimensional representation. This work compares meta-embeddings trained for different losses, namely loss functions that account for angular distance between the reconstructed embedding and the target and those that account normalized distances based on the vector length. We argue that meta-embeddings are better to treat the ensemble set equally in unsupervised learning as the respective quality of each embedding is unknown for upstream tasks prior to meta-embedding. We show that normalization methods that account for this such as cosine and KL-divergence objectives outperform meta-embedding trained on standard $\ell_1$ and $\ell_2$ loss on \textit{defacto} word similarity and relatedness datasets and find it outperforms existing meta-learning strategies.
翻译:近些年来,为改进分布式文字表达方式而整合字嵌入的词汇在自然语言处理任务中表现出了良好的成功。 这些方法或者对一组矢量进行直截了当的数学操作,或者使用未经监督的学习来寻找一个较低维度的表达方式。 这项工作比较了为不同损失而培训的元组成, 即考虑到重新嵌入器与目标之间的角距离以及根据矢量长度计算正常距离的损失功能。 我们争辩说, 元组合最好在未经监督的学习中同等对待组合, 因为每个嵌入物的各自质量在元化前的上游任务并不为人所知。 我们表明,考虑到这一点的正常化方法, 例如 cosine 和 KL- diverence 目标, 超越了按标准 $\ell_ 1 $ 和 $\ ell_ 2美元 所培训的元融合。 我们争论说, 元相近和关联性词汇数据集比现有的元学习战略要好得多。