Nonparametric C- and D-vine based quantile regression

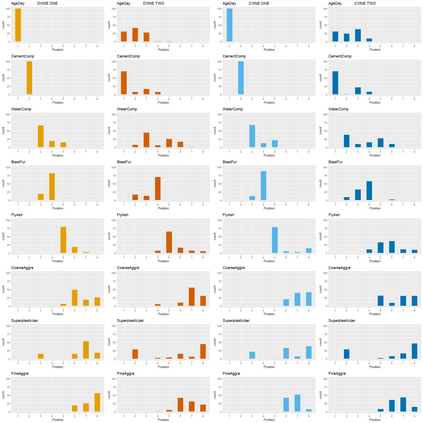
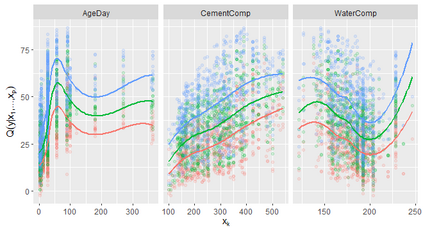
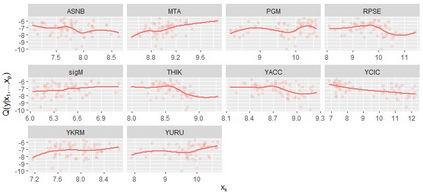
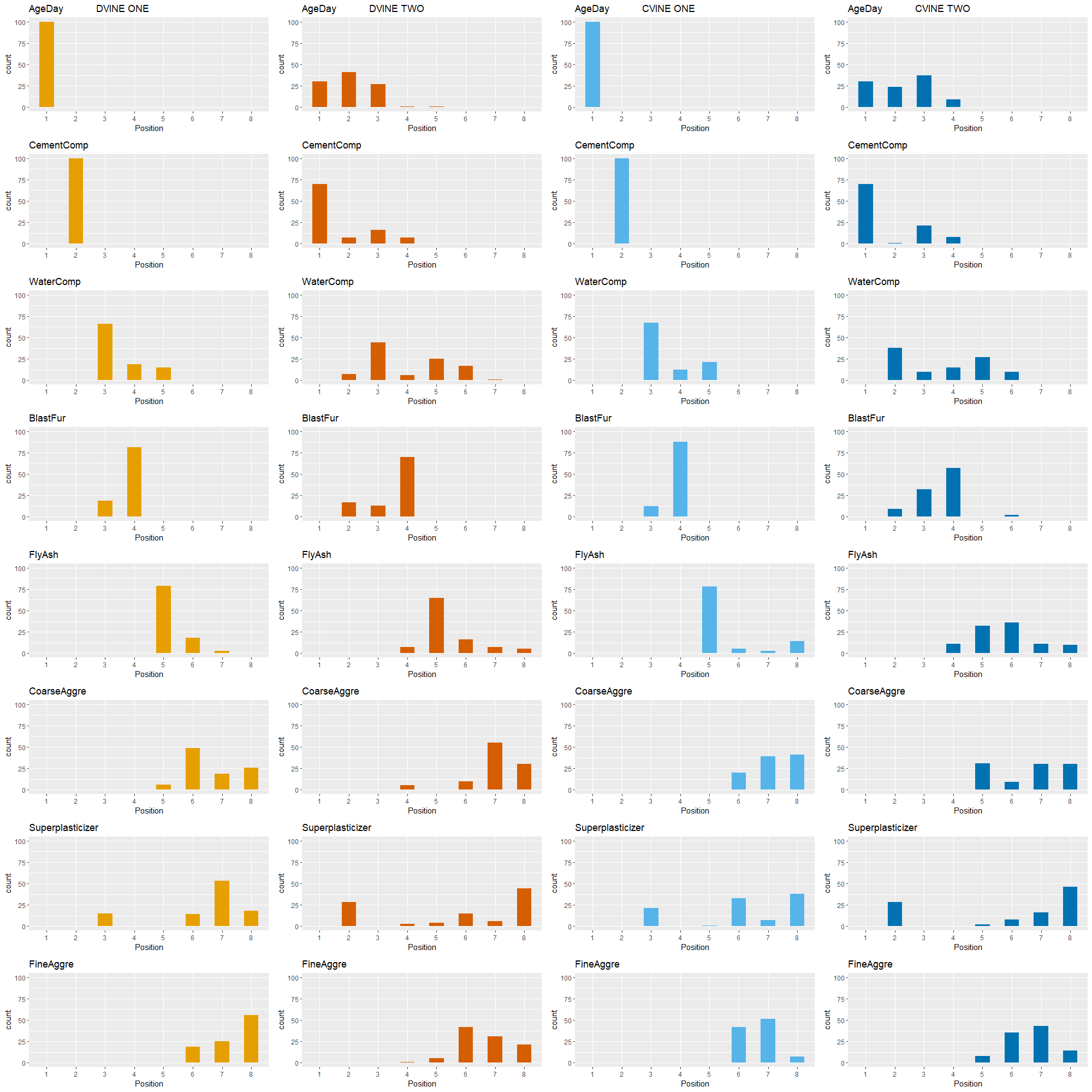
Quantile regression is a field with steadily growing importance in statistical modeling. It is a complementary method to linear regression, since computing a range of conditional quantile functions provides a more accurate modelling of the stochastic relationship among variables, especially in the tails. We introduce a novel non-restrictive and highly flexible nonparametric quantile regression approach based on C- and D-vine copulas. Vine copulas allow for separate modeling of marginal distributions and the dependence structure in the data, and can be expressed through a graph theoretical model given by a sequence of trees. This way we obtain a quantile regression model, that overcomes typical issues of quantile regression such as quantile crossings or collinearity, the need for transformations and interactions of variables. Our approach incorporates a two-step ahead ordering of variables, by maximizing the conditional log-likelihood of the tree sequence, while taking into account the next two tree levels. Further, we show that the nonparametric conditional quantile estimator is consistent. The performance of the proposed methods is evaluated in both low- and high-dimensional settings using simulated and real world data. The results support the superior prediction ability of the proposed models.