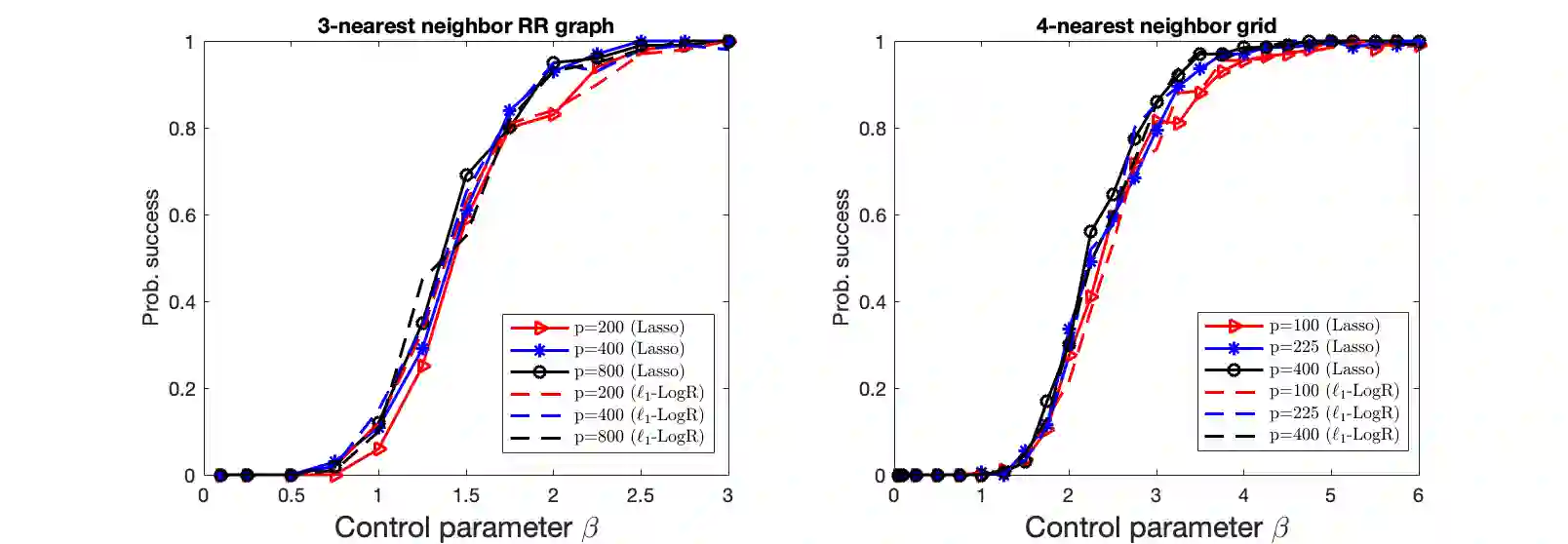
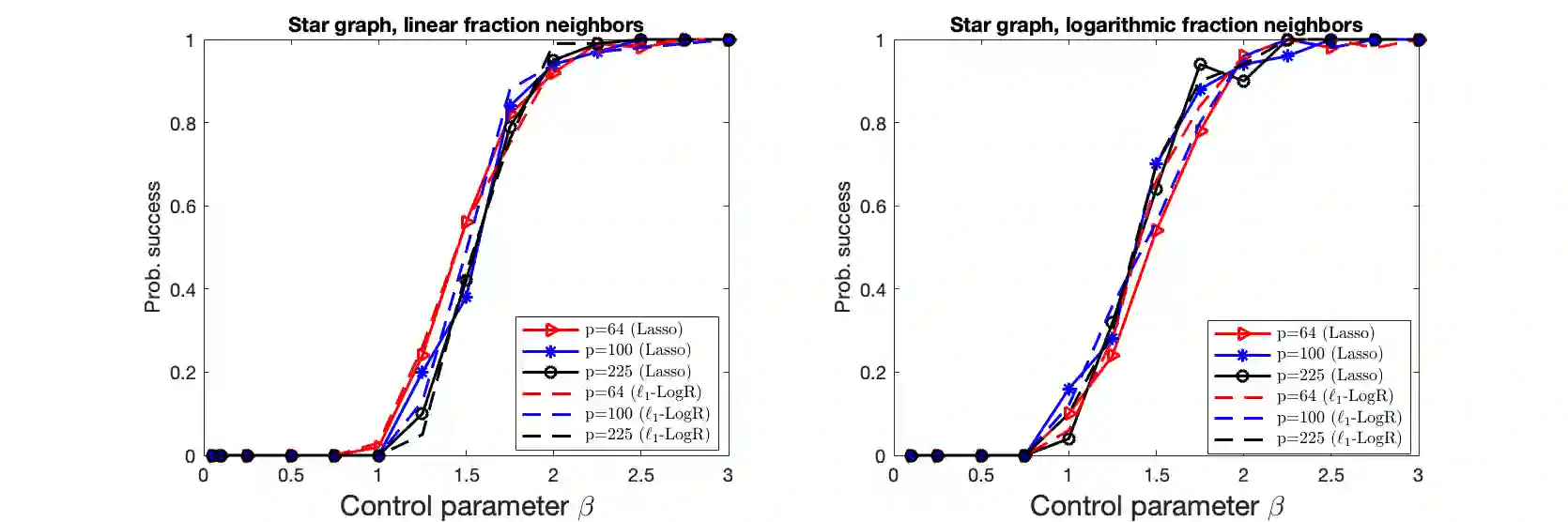
We consider the problem of high-dimensional Ising model selection using neighborhood-based least absolute shrinkage and selection operator (Lasso). It is rigorously proved that under some mild coherence conditions on the population covariance matrix of the Ising model, consistent model selection can be achieved with sample sizes $n=\Omega{(d^3\log{p})}$ for any tree-like graph in the paramagnetic phase, where $p$ is the number of variables and $d$ is the maximum node degree. The obtained sufficient conditions for consistent model selection with Lasso are the same in the scaling of the sample complexity as that of $\ell_1$-regularized logistic regression.
翻译:我们考虑了使用以邻里为基础的最小绝对缩水和选择操作员(Lasso)进行高维Ising模型选择的问题。 严格地证明,在Ising模型人口共变矩阵的某些温和的一致条件下,对于在抛磁阶段的任何类似树形图,只要以美元为变量,以美元为最高节点,就可实现一致的模式选择。 在与Lasso进行一致的模型选择方面,获得的足够条件在样本复杂性的尺度上与以美元为1的正规后勤回归相同。