Arbitrarily high-order energy-preserving schemes for the Zakharov-Rubenchik equation

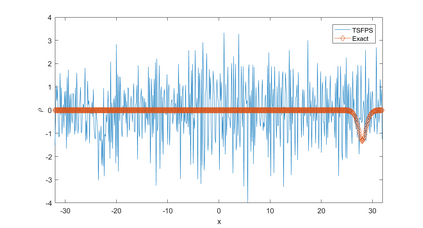
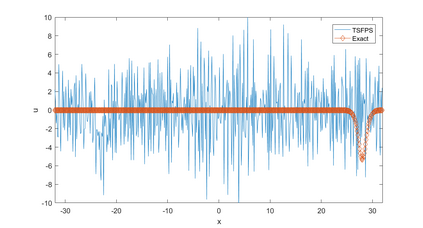
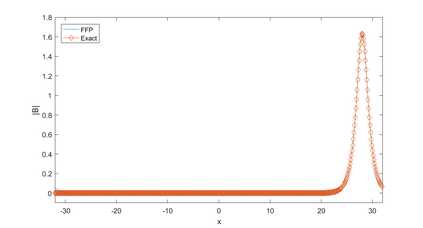
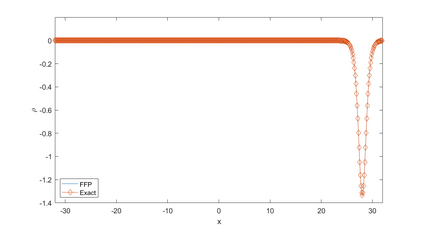
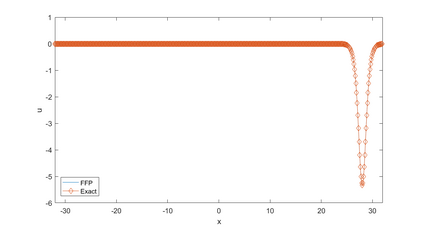
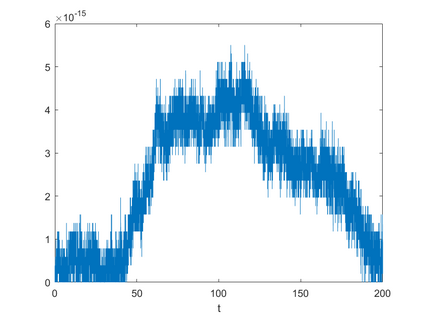
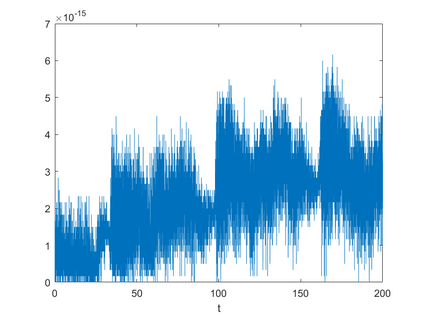
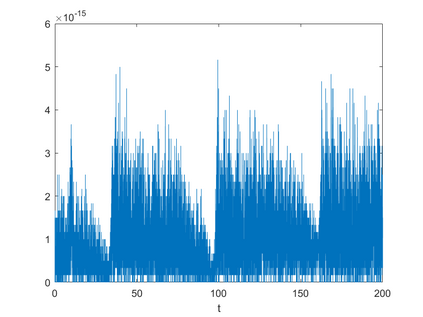
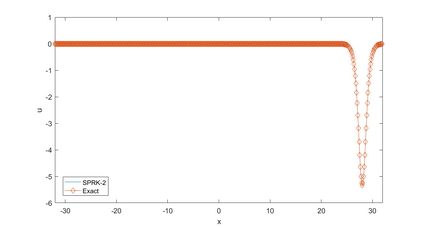
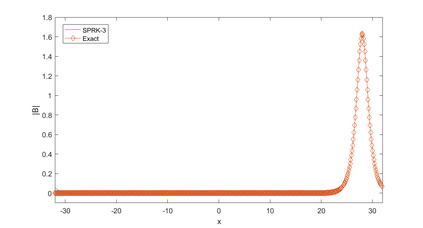
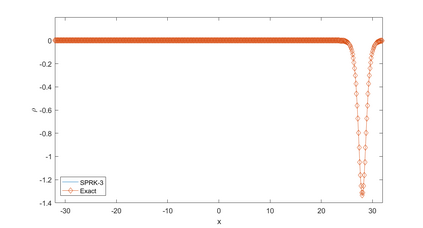
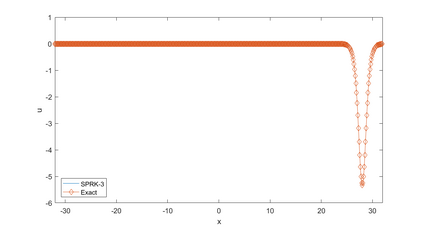
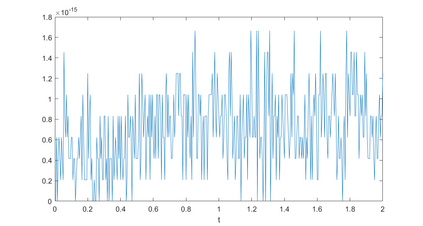
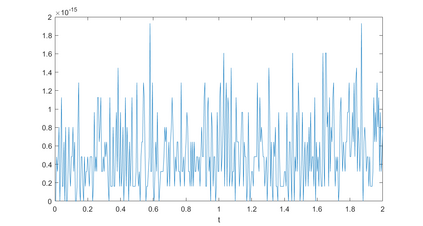
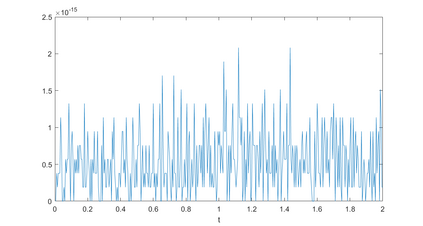
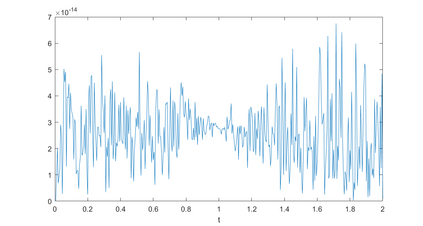
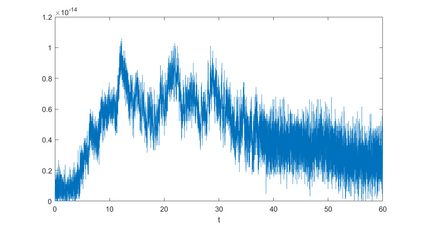
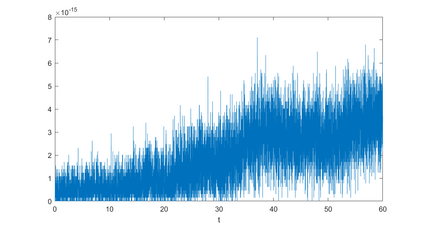
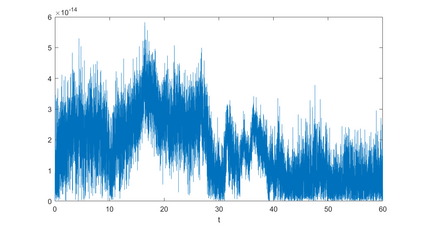
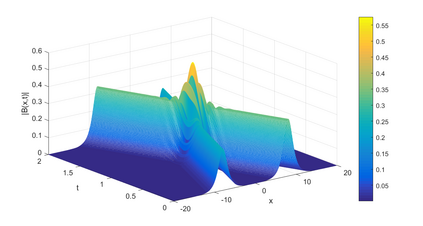
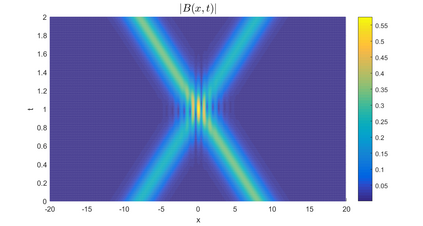
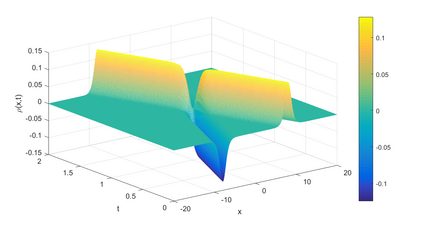
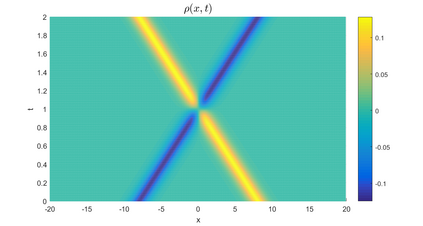
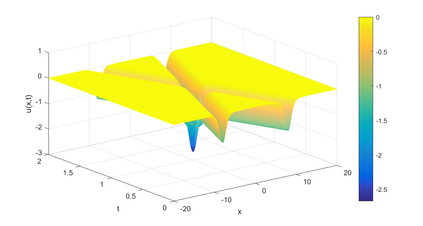
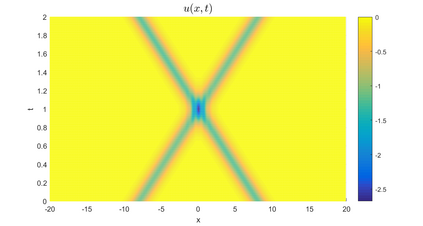
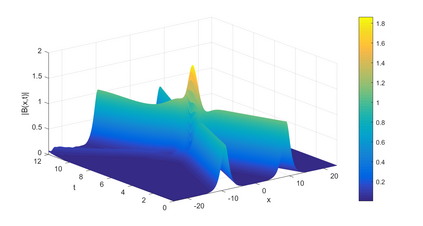
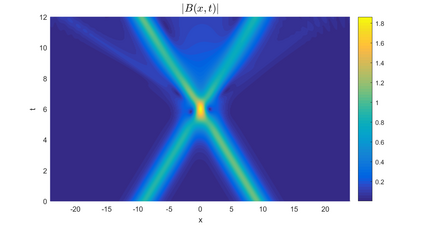
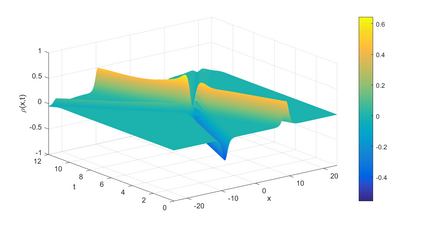
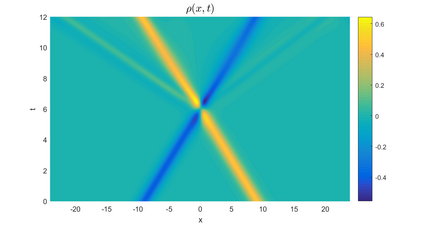
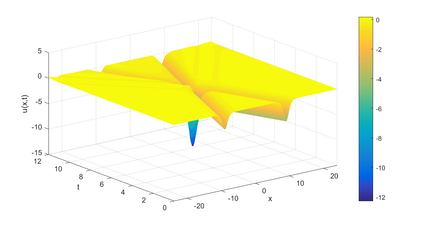
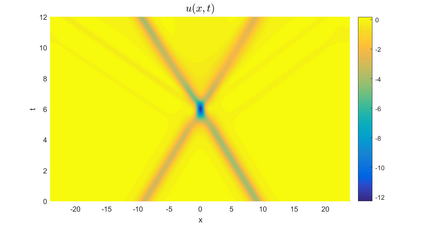
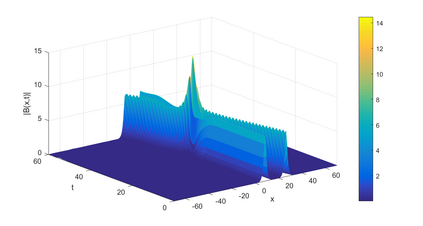
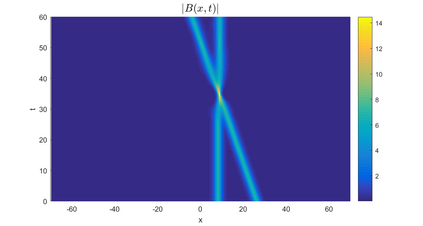
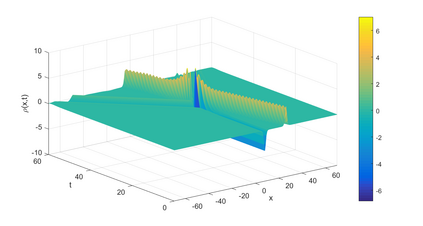
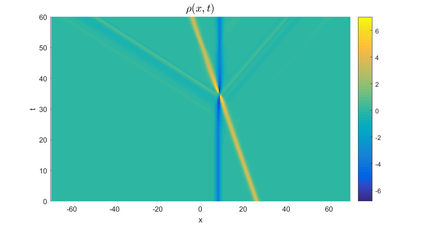
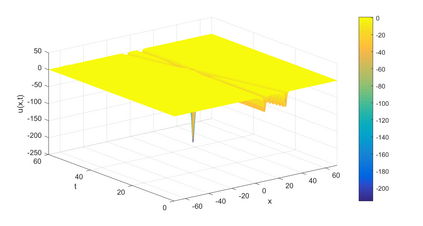
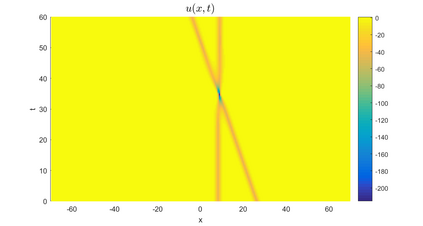
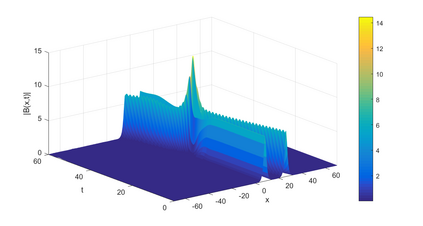
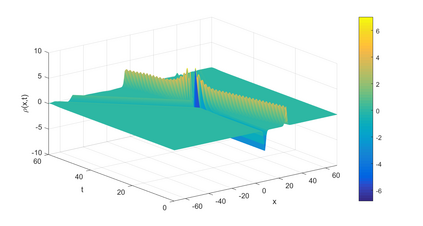
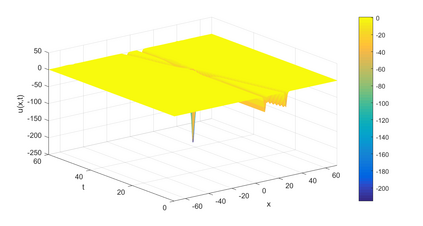
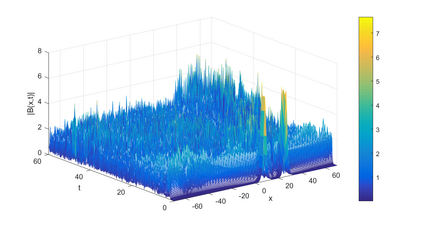
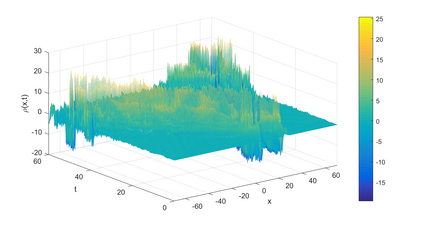
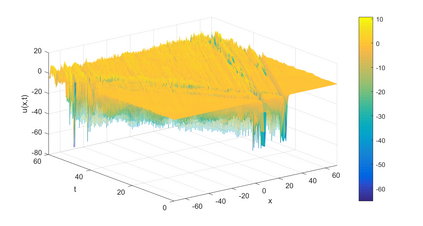
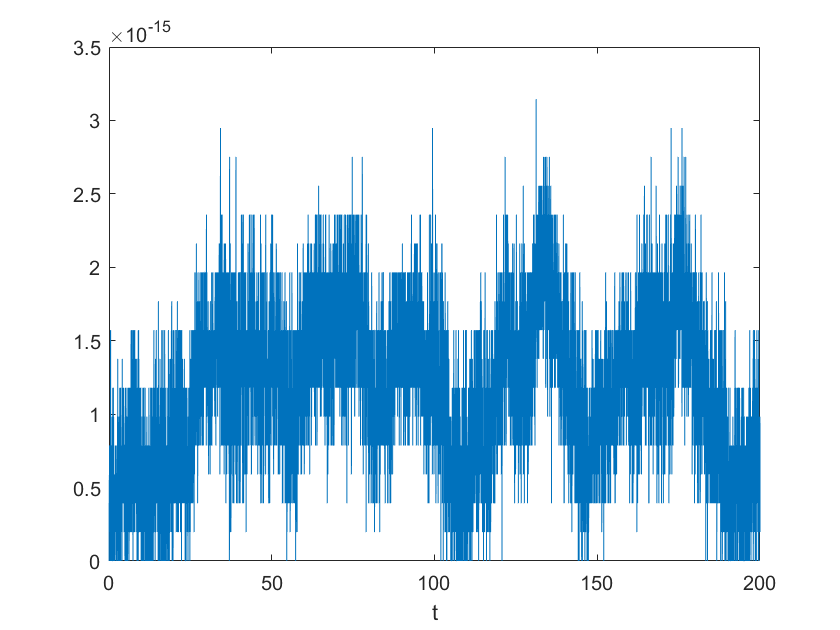
In this paper, we present a high-order energy-preserving scheme for solving Zakharov-Rubenchik equation. The main idea of the method is first to reformulate the original system into an equivalent one by introducing an quadratic auxiliary variable, and the symplectic Runge-Kutta method, together with the Fourier pseudo-spectral method is then employed to compute the solution of the reformulated system. The main benefit of the proposed method is that it can conserve the three invariants of the original system and achieves arbitrarily high-order accurate in time. In addition, an efficient fixed-point iteration is proposed to solve the resulting nonlinear equations of the proposed schemes. Several experiments are provided to validate the theoretical results.