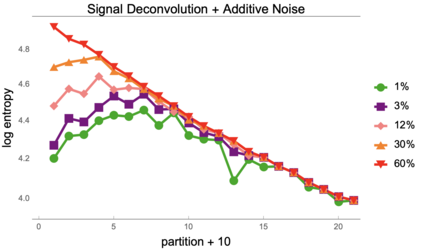
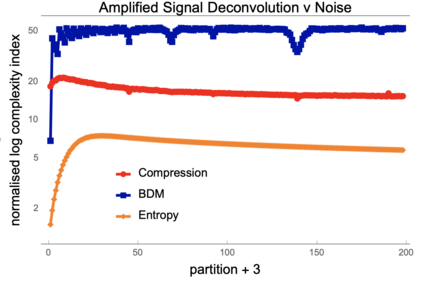
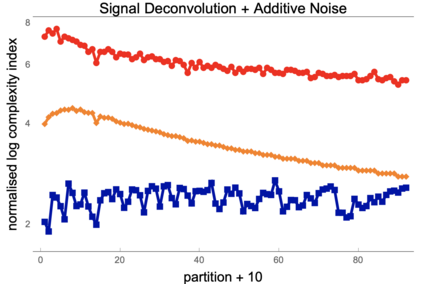
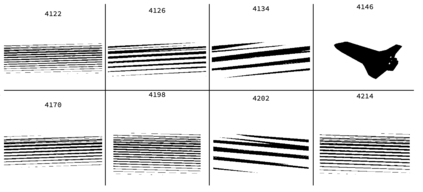
We introduce a general-purpose univariate signal deconvolution method based on the principles of an approach to Artificial General Intelligence. This approach is based on a generative model that combines information theory and algorithmic probability that required a large calculation of an estimation of a `universal distribution' to build a general-purpose model of models independent of probability distributions. This was used to investigate how non-random data may encode information about the physical properties such as dimension and length scales in which a signal or message may have been originally encoded, embedded, or generated. This multidimensional space reconstruction method is based on information theory and algorithmic probability, and it is agnostic, but not independent, with respect to the chosen computable or semi-computable approximation method or encoding-decoding scheme. The results presented in this paper are useful for applications in coding theory, particularly in zero-knowledge one-way communication channels, such as in deciphering messages sent by generating sources of unknown nature for which no prior knowledge is available. We argue that this can have strong potential for cryptography, signal processing, causal deconvolution, life, and techno signature detection.
翻译:我们介绍了一种基于人工通用智能方法的通用单变量信号反卷积方法。该方法基于将信息理论和算法概率相结合的生成模型,需要进行估计“通用分布”的大量计算,以构建与概率分布无关的模型模型。这一方法被用于研究非随机数据如何编码有关物理特性(如维度和长度尺度)的信息,其中信号或消息可能最初被编码、嵌入或生成。这种多维空间重构方法基于信息理论和算法概率,对所选择的可计算或半可计算的近似方法或编码-解码方案是不可知的,但不是独立的。本文提供的结果对编码理论尤其是零知识单向通信渠道非常有用,比如解密由未知性质的生成源发送的消息,对于此类消息没有任何先验知识。我们认为这对密码学、信号处理、因果反卷积、生命和技术标识检测具有极强的潜力。