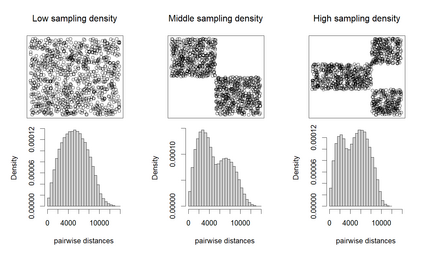
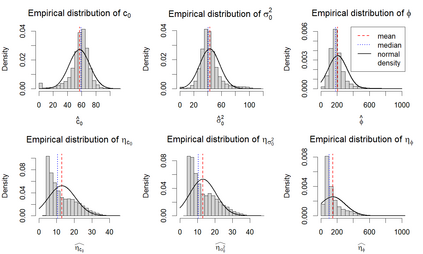
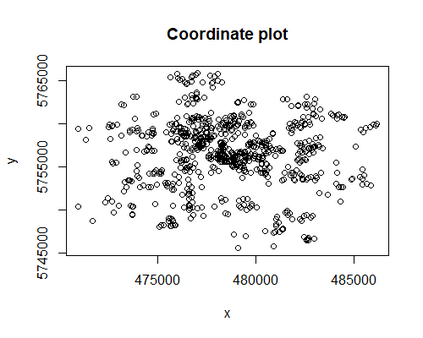
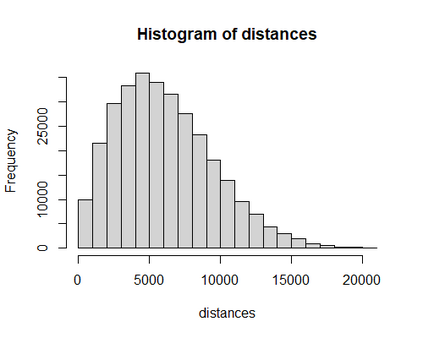
The estimation of parameter standard errors for semi-variogram models is challenging, given the two-step process required to fit a parametric model to spatially correlated data. Motivated by an application in the social-epidemiology, we focus on exponential semi-variogram models fitted to data between 500 to 2000 observations and little control over the sampling design. Previously proposed methods for the estimation of standard errors cannot be applied in this context. Approximate closed form solutions are too costly using generalized least squares in terms of memory capacities. The generalized bootstrap proposed by Olea and Pardo-Ig\'uzquiza is nonetheless applicable with weighted instead of generalized least squares. However, the standard error estimates are hugely biased and imprecise. Therefore, we propose a filtering method added to the generalized bootstrap. The new development is presented and evaluated with a simulation study which shows that the generalized bootstrap with check-based filtering leads to massively improved results compared to the quantile-based filter method and previously developed approaches. We provide a case study using birthweight data.
翻译:半变形模型的参数标准误差估计具有挑战性,因为要将参数模型与空间相关数据相适应,需要分两步程序。受社会流行病学应用的驱动,我们注重指数半变数模型,该模型可适应500至2000年的观测数据,对抽样设计几乎没有控制。以前提出的标准误差估计方法无法在此背景下适用。近似封闭形式解决方案使用记忆能力方面最差的平方,成本太高。Olea和Pardo-Ig\'uzquiza提出的通用靴子装置仍然适用加权而非通用最小方块。然而,标准误差估计极为偏差和不准确。因此,我们提议在通用靴子陷阱中增加一种过滤方法。新的开发经过模拟研究后得到介绍和评价,该模拟研究表明,带有基于检查的过滤器的通用靴子带与基于四分法的过滤法和先前制定的办法相比,其结果大为改善。我们提供了利用出生体重数据进行案例研究。