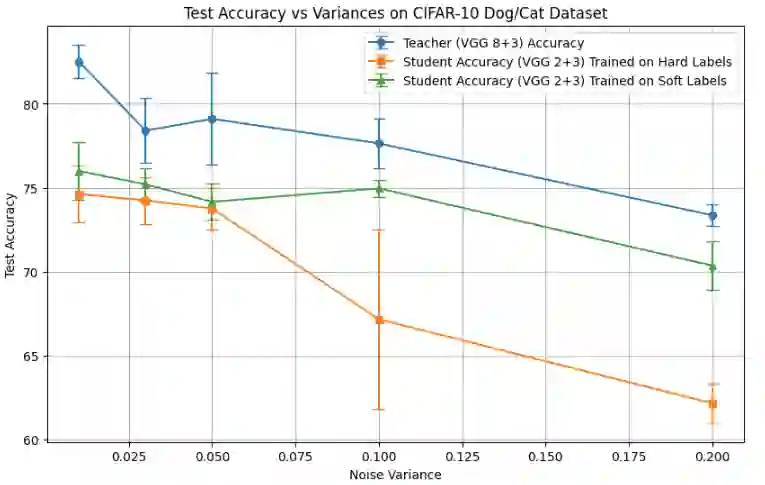
Knowledge distillation, where a small student model learns from a pre-trained large teacher model, has achieved substantial empirical success since the seminal work of \citep{hinton2015distilling}. Despite prior theoretical studies exploring the benefits of knowledge distillation, an important question remains unanswered: why does soft-label training from the teacher require significantly fewer neurons than directly training a small neural network with hard labels? To address this, we first present motivating experimental results using simple neural network models on a binary classification problem. These results demonstrate that soft-label training consistently outperforms hard-label training in accuracy, with the performance gap becoming more pronounced as the dataset becomes increasingly difficult to classify. We then substantiate these observations with a theoretical contribution based on two-layer neural network models. Specifically, we show that soft-label training using gradient descent requires only $O\left(\frac{1}{\gamma^2 \epsilon}\right)$ neurons to achieve a classification loss averaged over epochs smaller than some $\epsilon > 0$, where $\gamma$ is the separation margin of the limiting kernel. In contrast, hard-label training requires $O\left(\frac{1}{\gamma^4} \cdot \ln\left(\frac{1}{\epsilon}\right)\right)$ neurons, as derived from an adapted version of the gradient descent analysis in \citep{ji2020polylogarithmic}. This implies that when $\gamma \leq \epsilon$, i.e., when the dataset is challenging to classify, the neuron requirement for soft-label training can be significantly lower than that for hard-label training. Finally, we present experimental results on deep neural networks, further validating these theoretical findings.
翻译:暂无翻译